Home / Section index
 www.icosaedro.it 

 How to locate the celestial bodies in the sky

Updated: 2019-06-24

In this article we will show how to read the ephemeris tables and how to locate the celestial bodies by using a magnetic compass and the astrolabe we build in the previous article Celestial Navigation at Home.

Contents

Azimuth and Elevation of a celestial body

The Azimuth is the horizontal angular distance of the celestial body from the North direction. If that North is the geographic North Pole, then we have the Geographic Azimuth; if that North is the Magnetic North, then we have the Magnetic Azimuth. Since we will use a magnetic compass, this latter is the Azimuth we are dealing with.

The Elevation, or Altitude, of the celestial body is its angular distance from the horizon.

The lensatic magnetic compass can be used to locate a star of given magnetic Azimuth. The astrolabe we build in the previous article could be used to measure the Elevation over the horizont. In this article we show how to determine the position of the star by reading the ephemeris tables and performing some calculation.

Once the our position, the local magnetic variation, the Magnetic Azimuth and the Elevation of the celestial body are known, we can easily locate that celestial body in the sky by using our compass and astrolabe.

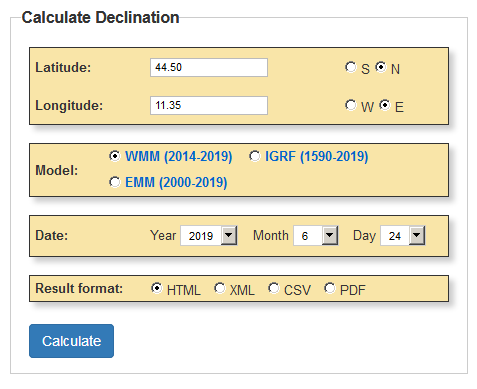
How to locate our geographical position

Our latitude and longitude can be obtained from several sources: from the world map, from a GPS receiver, or by visiting maps.google.com. In this latter case, the URL tells something like this:

 https://www.google.com/maps/@44.4950661,11.3535124,15z

where +44.50 is my latitude and -11.35 is my longitude; note how the sign of the longitude is reversed, but apart from that the longitude can be easily recognized anyway.

How to get the local magnetic variation

By definition, the Magnetic North is the direction of the projection of the Earth magnetic field vector on the horizontal plane. For this reason the needle of the magnetic compass is so thin and flat and must rotate freely over the horizontal plane. The Magnetic North does not coincide with the Geographic North, but instead it deviates more or less from it, either toward East or toward West. The amplitude of this deviation, also named magnetic variation, varies from site to site and varies over time, so it must be checked and updated periodically, at least every few months. The magnetic variation is positive if the needle of the compass deviates toward East respect to the Geographic North, and it is negative if it deviates toward West.

The Earth magnetic field is constantly measured and several mathematical models have been developed in an attempt to predict its evolution over time for any location in the world. For example, on https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml we can choose among several mathematical models and get the respective estimation of the magnetic variation. In my case I found:

The NOAA page allows us to calculate the current magnetic variation in our location. In the example of the figure the result is about 3° East, which means the needle of the the magnetic compass deviates 3° East from the real geographic North. This deviation must be accounted in order to accurately calculate the magnetic Azimuth of any star.

which finally tells the local magnetic variation I must account for today is +3.1° ± 0.3°. This value should then be re-checked again later, for example after some week or some month.

For more about the Earth magnetic field and the magnetic variation, see Magnetic declination (Wikipedia).

Reading ephemeridis for Sun, Moon, planets and stars

We will use the Nautical Almanac TheNauticalAlmanac.com we already see in the article before, where the positions of the Sun, of the Moon, of several planets and several stars are reported, day by day and hour by hour.

Reading ephemeris for Sun, Moon and planets

Locate the table of the ephemeris about the Sun for the day of interest, for example 2019-06-24 12:00 UTC:

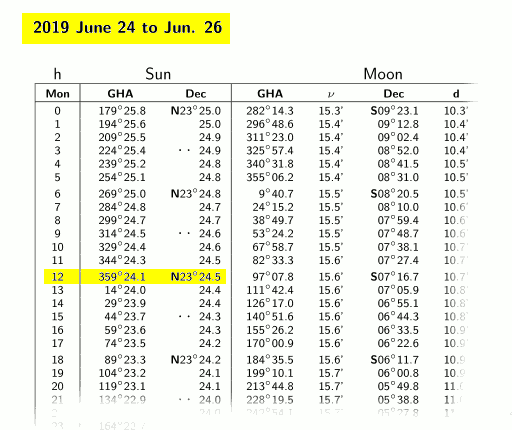
From the ephemeris of the Sun for the given date and time, we read the position of the Sun as Dec (that is latitude) and GHA (that is the longitude measured from the Greenwich meridian). Positions are reported for integral hours; in this case "12" means "12:00:00". The position of the Sun for fractional hour can be easily calculated by interpolation between two rows of the table.

The data we are interested to are highlighted in the figure above; it is convenient to translate a bit these number to fit our needs as we already shown in the previous article:

Sun_lat = N23° 24.5' = +23.41°
Sun_lon = 359° 24.1' GHA = 359.40° GHA = -0.60°

For the Moon and the planets we may proceed in the same exact way. For example, Saturn 2019-06-24 02:00 UTC:

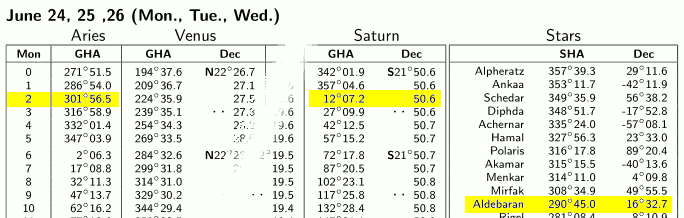
The ephemeris of Venus, Mars, Jupiter and Saturn are also reported. In our example we take Saturn; its GHA and Dec have the exact same meaning we already saw for the Sun.

Here again, we translate these numbers according to our convention obtaining:

Saturn_lat = S21° 50.6' = -21.84°
Saturn_lon = 12° 07.2' GHA = +12.12°

Reading ephemeris for stars

Locate the table for the stars for the days 24, 25 and 26 of June 2019:

The position of the "fixed" stars in the sky varies only slightly over time and it is mostly affected only by the rotation of the Earth around the polar axis. For this reason the ephemeris tables only report their position once every 3 days rather that hour by hour. Moreover, rather than their GHA, the SHA is reported instead, that is their longitude respect to the celestial zero meridian, or Aries meridian. The Aries meridian joins the celestial North Pole to the Aries point where the Ecliptic crosses the celestial equator at the vernal equinox. The GHA of the Star for the given date and time can finally be calculated as the sum of the SHA of the star (about 290°) and the GHA of the Aries point for the given date and time (about 301°).

Note that there is just only one single table for the entire period of three days. This is because the location of the stars in the sky changes so slowly over time that them are also referred as fixed stars, although nothing is fixed in the Universe. Anyway, the "Dec" column reports the latitude just like we saw for Sun and planets, while the SHA column reports the sidereal hourly angle rather that the GHA (Greenwich hourly angle). The SHA is just like the GHA but the angle is measured respect to the meridian of Aries (or γ) point. The GHA of the star is then the sum of its SHA and the GHA of Aries at the given date and time: 

Star_GHA = Star_SHA + Aries_GHA

The result of the formula above must be normalized to the range [0°,360°[, so if it's greater or equal to 360°, subtract 360°. The GHA of the star can then be easily converted to its longitude: 

Star_lon = Star_GHA         if  Star_GHA ≤ 180°
Star_lon = 360° - Star_GHA  if  Star_GHA > 180°

In our example , the current GHA of Aries is reported in the table to the left in the same page:

Aries_GHA = 301° 56.5'

Lets take for example Aldebaran. Its latitude can be read straight from the table, while its longitude must be calculated by adding its SHA (more or less "fixed") to the current GHA of Aries: 

Aldebaran_lat = 16° 32.7' = +16.55

Aldebaran_lon = Aldebaran_SHA + Ariete_GHA
              = 290° 45.0'    + 301° 56.5'    (replacing numbers in formula)
              = 290.75°       + 301.94°       (converting to decimal degrees)
              = 592.69°                       (performing addition)
              = 232.69°                       (normalizing GHA to the [0°,360°[ range)
              = -127.31°                      (normalizing lon to the [-180°,+180°[ range)

Computing Azimuth and Elevation of the celestial body

Now that our position P and the position of the celestial body S are known, it's a matter to solve the spherical triangle with vertices P, S and N (the North Pole):

All the parameters of the spherical triangle: N = North Pole; P = our position; S = star position. Left: the star is West respect to our position; right: the star is East. Note that the Azimuth Saz of the start S respect to our position P is by definition the clockwise angle measured starting from the arc of meridian PN that joins our position to the North Pole; for that reason in the case to the right the Azimuth is simply the spherical angle A, while in the case to the left the complementary angle 360°-A must be taken instead.

Two sides 90°-Slat and 90°-Plat, and the included angle |Slat-Plat| are known. From them we may calculate all the remaining elements of the spherical triangle PSN, that is the opposite side 90°-Selev and the spherical angle in P giving the Geographic Azimut of the star. Care must be paid to the longitudes of S and P, as the Azimuth changes depending from their relative positions (ence the two drawings above). For the details of the calculation, see for example https://en.wikipedia.org/wiki/Spherical_trigonometry. To the Geographic Azimuth we must subtract the local magnetic variation to obtain the Magnetic Azimuth; the elevation should be corrected for the atmospheric refraction.

The details of the calculation are quite boring and are summarized briefly here below: 

If Slon > Plon:  A = Slon - Plon  and  star_west = true
If Slon ≤ Plon:  A = Plon - Slon  and  star_west = false
If A > 180°:  A = 360° - A   and  star_west = NOT star_west
c = 90° - Slat
b = 90° - Plat
a = acos( cos(b) cos(c) + sin(b) sin(c) cos(A) )
s = (a + b + c)/2
C = 2 asin( sqrt( (sin(s-a) sin(s-b)) / (sin(a) sin(b)) ) )
If star_west is true:  Saz = 360° - C
If star_west is false: Saz = C
Sazmag = Saz - Pmagvar
Selev = 90° - a

where Saz il the geographic Azimuth of the star, Sazmag is its magnetic Azimuth, and Pmagvar is the local magnetic variation, positive East.

The page Star Relative Location Calculator can do all these calculations for you. Enter the position, the local magnetic variation, and the position of the celestial body (for example, Saturn):

and then press the Compute button to get:

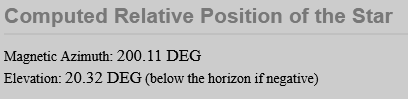
Final result: the day 2019-06-24 02:00 UTC, Saturn will be visible in the sky at 200° magnetic azimuth, 20° over the horizon.

References
Umberto Salsi
Comments
Contact
Site map
Home / Section index
Still no comments to this page. Use the Comments link above to add your contribute.