Home / Indice sezione
 www.icosaedro.it 

 Come individuare gli astri nel cielo

Aggiornato: 2019-06-24

In questo articolo mostriamo come leggere le effemeridi e come individuare gli astri nel cielo usando la bussola e l'astrolabio costruito nell'articolo precedente Navigazione Astronomica da Casa.

Sommario

Azimut ed elevazione di un astro

L'Azimut è la direzione in cui appare l'astro misurata come angolo rispetto al Nord. Se il Nord è quello geografico allora avremo l'Azimut Geografico; se il Nord è quello magnetico allora avremo l'Azimut Magnetico. Siccome useremo una bussola magnetica per individuare il Nord Magnetico, è quest'ultimo tipo di Azimut che useremo.

L'Elevazione o altezza dell'astro è la sua distanza angolare dall'orizzonte.

La bussola magnetica si può usare per localizzare un astro di Azimut dato. L'astrolabio che abbiamo costruito nell'articolo precedente si può usare per misurare l'Elevazione sopra l'orizzonte. In questo articolo mostriamo come determinare la posizione dell'astro leggendo le effemeridi e facendo qualche calcolo.

Una volta noti la nostra posizione geografica, la variazione magnetica locale, l'Azimut Magnetico e l'Elevazione dell'astro, sarà quindi possibile individuarlo nel cielo usando la bussola magnetica e l'astrolabio.

Determinare la nostra posizione geografica

La nostra latitudine e longitudine si possono ricavare dalle carte geografiche, da un ricevitore GPS, oppure consultando il servizio maps.google.com; in quest'ultimo caso, basta leggere l'URL. Nel mio caso:

 https://www.google.com/maps/@44.4950661,11.3535124,15z

che fornisce latitudine +44.50 e longitudine -11.35; notare che il segno della longitudine è invertito rispetto alla nostra convenzione.

Determinare la variazione magnetica locale

Per definizione, il Nord Magnetico è la direzione della proiezione orizzontale del campo magnetico locale. Per questo motivo l'ago della bussola è piatto e deve ruotare liberamente sul piano orizzontale. Il Nord Magnetico non coincide con il Nord Geografico ma può essere più o meno deviato verso Est o verso Ovest. L'entità di questa deviazione si chiama variazione magnetica o declinazione magnetica. La variazione magnetica cambia di luogo in luogo e cambia anche nel tempo. Per esempio, la variazione magnetica media in Italia nei primi anni 2000 era di circa 1 grado Est; oggi nel 2019 è di circa 3 gradi Est e cresce ancora. La variazione magnetica è positiva se l'ago della bussola devia verso Est rispetto al Nord geografico, ed è negativa se l'ago della bussola devia verso Ovest rispetto al Nord geografico.

Il campo magnetico terrestre viene costantemente monitorato. Sono anche disponibili modelli matematici che permettono di calcolarne il valore punto per punto. Ad esempio, la pagina https://www.ngdc.noaa.gov/geomag/calculators/magcalc.shtml:

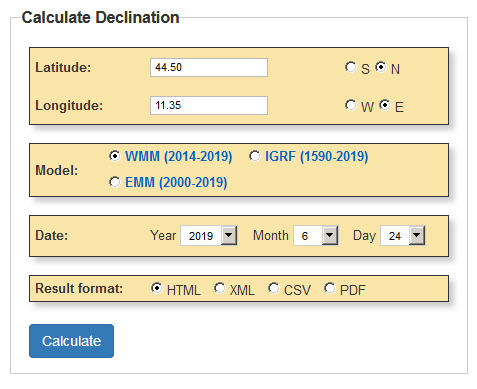
La pagina del NOAA permette di calcolare la variazione magnetica corrente nella nostra posizione. Nell'esempio della figura il risultato è di circa 3° Est, che significa l'ago della bussola magnetica devia 3° Est dal Nord geografico. Occorre tener conto di questa deviazione per calcolare accuratamente l'Azimut magnetico degli astri.

nel mio caso oggi fornisce una variazione magnetica di +3.1° ± 0.3°. Dovremo ri-controllare questo valore ogni qualche mese.

Per approfondire: Magnetic declination (Wikipedia).

Leggere le effemeridi per Sole, Luna, pianeti e stelle

Useremo le effemeridi pubblicate da The Nautical Almanac TheNauticalAlmanac.com, versione completa, che riporta la posizione del Sole, della Luna, di alcuni pianeti e di alcune stelle.

Leggere le effemeridi per Sole, Luna e Pianeti

Individuare la tabella delle effemeridi del Sole per il giorno, per esempio 2019-06-24 alle ore 12:00 UTC (14:00 CEST):

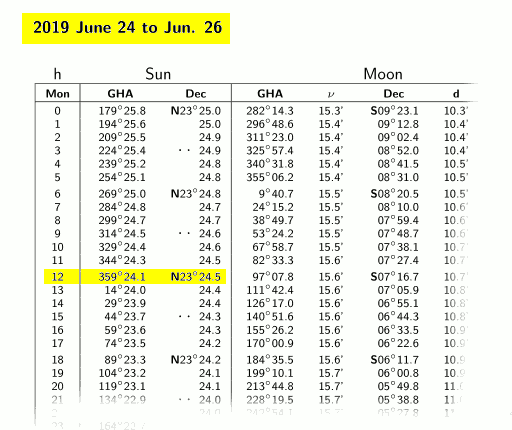
Dalle effemeridi del Sole per il giorno e ora dati, leggiamo la posizione del Sole come Dec (cioè latitudine) e GHA (cioè longitudine misurata dal meridiano di Greenwich). Le posizioni sono riportate per ore intere; in questo caso "12" significa "12:00:00". La posizione del Sole per frazioni di ora si può facilmente calcolare per interpolazione tra due righe della tabella.

Prendo nota della latitudine e della longitudine del Sole e le esprimo secondo la nostra convenzione:

Sole_lat = N23° 24.5' = +23.41°
Sole_lon = 359° 24.1' GHA = 359.40° GHA = -0.60°

Per la Luna e per i pianeti si procede nello stesso modo. Ad esempio, Saturno 2019-06-24 02:00 UTC:

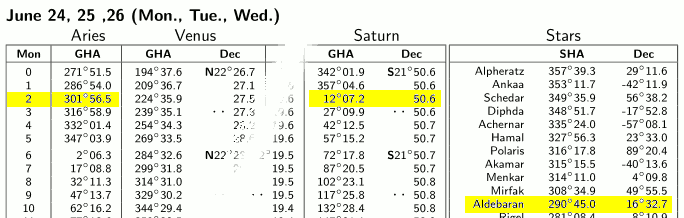
Vengono riportate anche le effemeridi di Venere, Marte, Giove e Saturno. Nel nostro esempio consideriamo Saturno; il suo GHA e Dec hanno lo stesso esatto significato che abbiamo visto per il Sole.

Prendo nota della latitudine e della longitudine di Saturno e le esprimo secondo la nostra convenzione:

Saturno_lat = S21° 50.6' = -21.84°
Saturno_lon = 12° 07.2' GHA = +12.12°

Leggere le effemeridi per le stelle

Individuo la tabella delle effemeridi per le stelle nel periodo 24, 25, 26 giugno 2019:

La posizione della stelle "fisse" nel cielo cambia solo leggermente nel tempo ed è per lo più influenzata solo dalla rotazione della Terra intorno all'asse polare. Per tale motivo le effemeridi riportano la loro posizione solo ogni tre giorni invece che ora per ora. Inoltre, invece che il loro GHA, viene riportato il loro SHA, cioè la loro longitudine rispetto al meridiano celeste zero, o meridiano dell'Ariete. Il meridiano dell'Ariete unisce il Polo Nord celeste al punto dell'Ariete dove l'Eclittica interseca l'equatore celeste all'equinozio vernale. Il GHA della stella per il giorno e l'ora date si può finalmente calcolare come somma tra l'SHA della stella (circa 290°) e il GHA del punto dell'Ariete per il girono e l'ora (circa 301°).

Notare che c'è una sola tabella per il periodo di 3 giorni, e notare che le coordinate delle stelle cambiano poco o nulla nel corso di un anno. La latitudine delle stelle ha lo stesso significato della latitudine per il Sole e i Pianeti. La longitudine delle stelle, invece, viene riportata come SHA (sidereal hourly angle) perché il meridiano di riferimento non è il meridiano di Greenwich, ma il meridiano che passa per il punto dell'Ariete, detto anche punto Gamma (γ). Il GHA della stella è quindi la somma del suo SHA e del GHA di Ariete nel giorno e all'ora dati: 

Star_GHA = Star_SHA + Aries_GHA

Il risultato della formula sopra deve essere normalizzato al range [0°,360°[, così se è maggiore o uguale a 360°, sottrarre 360°. Il GHA della stella si può quindi facilmente convertire nella sua longitudine: 

Star_lon = Star_GHA         se  Star_GHA ≤ 180°
Star_lon = 360° - Star_GHA  se  Star_GHA > 180°

Nel nostro esempio il GHA corrente del punto dell'Ariete è

Ariete_GHA = 301° 56.5'

Le coordinate di Aldebaran sono quindi la latitudine letta dalla tabella, e la longitudine ottenuta sommando l'SHA della stella al GHA dell'Ariete: 

Aldebaran_lat = 16° 32.7' = +16.55

Aldebaran_lon = Aldebaran_SHA + Aries_GHA
              = 290° 45.0'    + 301° 56.5'   (sostituisco numeri in formula)
              = 290.75°       + 301.94°      (converto in gradi decimali)
              = 592.69°                      (calcolo addizione)
              = 232.69°                      (normalizzo GHA al range [0°,360°[)
              = -127.31°                     (normalizzo lon al range [-180°,+180°[)

Calcolare Azimut ed Elevazione dell'astro

Una volta noti la nostra posizione P e la posizione dell'astro S, si tratta di risolvere il triangolo sferico formato dai punti P, S e N (Polo Nord):

Tutti i parametri del triangolo sferico: N = Polo Nord; P = la nostra posizione; S = la posizione dell'astro. A sinistra: l'astro è a Ovest rispetto alla nostra posizione; a destra: l'astro è a Est rispetto alla nostra posizione. Notare che l'Azimut Saz dell'astro rispetto alla nostra posizione P è per definizione l'angolo in senso orario misurato a partire dall'arco di meridiano PN che unisce la nostra posizione al Polo Nord; per questa ragione nel caso a destra l'Azimut è semplicemente l'angolo sferico A, mentre nel caso a sinistra bisogna prendere l'angolo complementare 360°-A.

Sono dati due lati 90°-Slat e 90°-Plat, ed è dato l'angolo compreso |Slat-Plat|. Da questi si possono ricavare gli altri elementi del triangolo sferico PSN, e cioè il lato opposto 90°-Selev e l'angolo sferico in P che dà l'azimut geografico dell'astro. Bisogna fare attenzione ai casi in cui la longitudine di S viene prima o dopo P, ecco il perché dei due disegni qui sopra. Per i dettagli del calcolo si può vedere https://en.wikipedia.org/wiki/Spherical_trigonometry. All'azimut geografico bisogna sottrarre la variazione magnetica locale per ottenere l'azimut magnetico; l'elevazione si può correggere per l'effetto di rifrazione atmosferica.

I dettagli del calcolo sono abbastanza noiosi e sono riassunti di seguito: 

If Slon > Plon:  A = Slon - Plon  and  star_west = true
If Slon ≤ Plon:  A = Plon - Slon  and  star_west = false
If A > 180°:  A = 360° - A   and  star_west = NOT star_west
c = 90° - Slat
b = 90° - Plat
a = acos( cos(b) cos(c) + sin(b) sin(c) cos(A) )
s = (a + b + c)/2
C = 2 asin( sqrt( (sin(s-a) sin(s-b)) / (sin(a) sin(b)) ) )
If star_west is true:  Saz = 360° - C
If star_west is false: Saz = C
Sazmag = Saz - Pmagvar
Selev = 90° - a

dove Saz è l'Azimut geografico dell'astro, Sazmag è il suo Azimut magnetico, e Pmagvar è la variazione magnetica locale, positiva Est.

La pagina Calcolatore della posizione relativa dell'astro può fare tutti questi calcoli per te. Inserire la posizione, la variazione magnetica del luogo, la posizione dell'astro (per esempio, Saturno) e premere il pulsante Compute:

per ottenere:

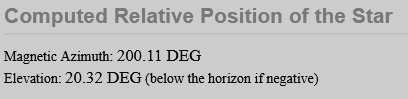
Quindi la notte del 2019-06-24 02:00 UTC, Saturno sarà visibile ad un azimut magnetico di 200° e ad una altezza di 20° sopra l'orizzonte.

Riferimenti
Umberto Salsi
Commenti
Contatto
Mappa
Home / Indice sezione
Still no comments to this page. Use the Comments link above to add your contribute.