
| Home / Indice sezione | www.icosaedro.it |  |
 Le virate standard
Le virate standardUltimo aggiornamento: 2018-01-06
Cambiare rotta con un aeroplano richiede molta attenzione, perché le variabili in gioco sono tante ed è difficile seguire un percorso stabilito, soprattutto in fase di avvicinamento a una pista. Inoltre il pilota si trova spesso a dover eseguire delle manovre in assenza di riscontri esterni: il buio della notte, le nuvole, la foschia, la pioggia e l'alta quota sono tutti fattori che rendono difficile intuire l'assetto dell'aereo. Il pilota deve quindi affidarsi agli strumenti ed eseguire precise manovre pianificate in anticipo. In questo documento vediamo alcune manovre di virata standard.
Cos'è una virata standard
Facciamo una prova
Virate coordinate
Eseguire le virate in pratica
Considerazioni sulla geometria della virata
Verifichiamo le nostre virate
Inversione di rotta
Virata sul fix point
Virata sul VOR/DME
Uscire dal radiale di un VOR/DME su di una rotta stabilita
Immettersi sul radiale di un VOR/DME
Immettersi sul radiale del VOR dopo averlo intercettato
Conclusioni
Guidare un'automobile è intuitivo perché si ha sempre un riscontro immediato degli effetti delle azioni sul volante. Al contrario, a bordo dell'aereo spesso mancano riferimenti visivi precisi per calibrare le manovre, per cui bisogna affidarsi agli strumenti e alle nozioni. Le considerazioni che faremo qui, oltre che fornire ricette, aiutano a capire quali sono gli spazi di manovra del nostro aereo e quindi aiutano a pianificare meglio le nostre manovre.
Le virate servono per cambiare la direzione di marcia e si eseguono inclinando l'aereo a destra o a sinistra a seconda che si voglia virare a destra o a sinistra. L'aereo si inclina per effetto degli alettoni posti sulle ali: per inclinare l'aereo a destra, l'alettone di destra si alza e quello di sinistra si abbassa. L'effetto combinato delle forze risultanti è quello di far compiere all'aereo un arco di circonferenza. Notare che il timone di coda (rudder) non serve per virare, ma semmai serve per coordinare la virata (vedremo i dettagli in seguito).
La conseguenza della virata è l'aumento della resistenza aerodinamica e la perdita di quota. Questi due effetti vanno compensati in due modi: aumentando la potenza del motore e puntando il muso dell'aereo più in alto (cosa che comporta un ulteriore aumento della resistenza aerodinamica e una potenza ancora maggiore del motore). Una virata "ben fatta" dovrebbe consentire di:
Solo se queste condizioni sono rispettate, l'aereo descriverà un arco di circonferenza perfetto e potremo applicare le regole di virata che vedremo.
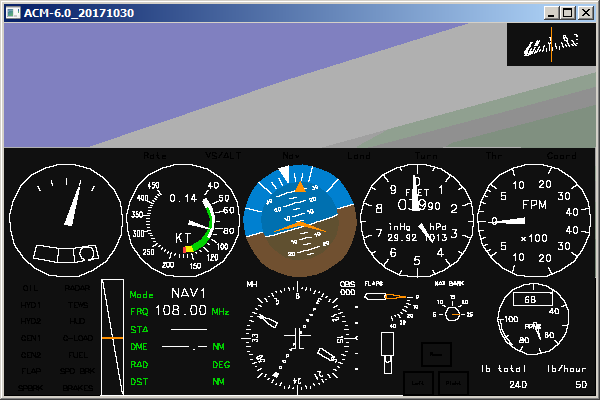
Proviamo una virata a 1,5°/s con il C-172RG del nostro simulatore. Portare l'aereo ad una quota di sicurezza appropriata, in modo che eventuali errori di manovra non ci portino subito allo schianto. 4000 ft potrebbe essere un valore adatto. Portare l'aereo a un volo livellato e a velocità costante di 80 kt. A questo punto muoviamo il mouse a destra in modo che l'aereo si inclini. L'indicatore della velocità di virata dovrebbe spostarsi sulla prima tacca. Nel frattempo l'aereo comincia a perdere quota, per cui dovremo anche tirare il mouse verso di noi. L'effetto risultante è che l'aereo perde velocità rapidamente e, se non interveniamo subito, rischieremo lo stallo. Premere quindi il tasto 3 per aumentare la potenza fino a che la velocità si mantiene stabilmente sugli 80 kt. A questo punto agire solo col mouse correggendo il pitch e il roll in modo che quota e velocità di virata rimangano costanti (rispettivamente, 4000 ft e 1,5°/s). La figura qui sotto mostra la situazione:
|
Virata (scoordinata) a destra a 1,5°/s, 80 kt, 4000 ft. Notare che la pallina dell'indicatore di virata è spostata a destra ad indicare una forte accelerazione laterale, e che la bussola magnetica è disallineata rispetto all'orizzonte visibile dal finestrino. |
All'inizio è difficile mantenere costanti tutti i parametri di volo, ma dopo qualche aggiustamento l'aereo dovrebbe stabilizzarsi e continuare la virata senza bisogno di correzioni. Mantenendo questo rateo di virata, l'aereo compie un giro di 360° in 360/1,5=240 s, cioè 4 minuti, ovvero 180° in due minuti. Provare a cronometrare per credere.
L'indicatore di rateo di virata (turn rate indicator) prevede anche una seconda tacca corrispondente a 3°/s. Questo rateo non può essere mantenuto neppure con il motore al massimo. Vedremo nel prossimo paragrafo perché.
Abbiamo sperimentato che è difficile mantenere una virata a 1.5°/s con il C-172RG, e che è impossibile raggiungere i 3°/s. Per capire il motivo dobbiamo esaminare la dinamica della virata e introdurre l'uso dell'indicatore di sbandamento e del timone.
La dinamica della virata è determinata da due forze: il peso del veicolo (mg, diretto verso il centro della Terra), e la portanza P (diretta come la normale al piano alare). Durante il volo orizzontale la portanza bilancia il peso. Durante la virata, invece, l'angolo di bank B fa sì che la portanza generi anche una forza laterale P sin(B), che è la forza centripeta che mantiene l'aereo sull'orbita circolare di raggio r. La componente verticale della portanza, P cos(B), deve bilanciare il peso dell'aereo.
Il modulo della portanza deve crescere di un fattore 1/cos(B), cosa che richiede quindi un maggiore pitch e una maggiore potenza del motore. In altri termini, dal punto di vista del motore e delle ali, durante la virata è come se il peso dell'aereo fosse aumentato del fattore che abbiamo detto. Questo fatto pone un limite all'angolo di bank massimo tollerabile dall'aereo, dipendente dalla potenza del motore e dalla robustezza delle strutture.
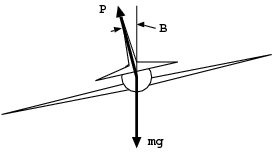
In formule:
P sin(B) = m r w2 = m v wP cos(B) = mg
Il rapporto tra queste due equazioni dà la relazione tra l'angolo di bank, la velocità lineare e la velocità angolare:
tan(B) =
v w g
Ad esempio, con una velocità lineare di 100 knots e una velocità angolare di 3°/s, si ottiene un angolo di bank di 15°. Il grafico qui sotto mostra gli angoli di bank in funzione della velocità per mantenere una velocità di virata di 1,5 gradi/s (linea continua) e di 3 gradi/s (linea tratteggiata):
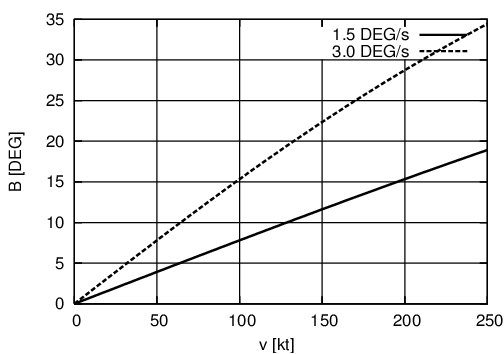
Angolo di bank alle diverse velocità.
Ogni aereo manovra a velocià tipiche predefinite, per cui di solito basta memorizzare uno o due angoli. Per il nostro C-172RG potremmo scegliere 80 kt come velocità tipica per le manovre di precisione. Guardando il grafico qui sopra si nota che la curva relativa ai 3°/s è quasi retta e molto vicina alla formula B=0,15*v. Questo calcolo si può eseguire a mente con questa regoletta:
|
Regola per calcolare a mente l'angolo di bank di una virata standard: prendere il valore della velocità espresso in kt, togliere l'ultima cifra a destra e aggiungere al risultato metà di sè stesso. Per virate non-standard al rateo di 1,5°/s basta prendere la metà dell'angolo ottenuto. |
Ad esempio, per v=100 kt si elimina lo zero finale e rimane 10; a questo numero sommo la sua metà ottenendo B=15° che corrisponde esattamente al valore del grafico.
Allora sono decollato con il mio C-172RG virtuale, sono salito a 3000 ft. Per cominciare con le cose facili ho iniziato una virata a soli 1,5°/s, a 80 knots. Una volta stabilizzato l'aereo, l'indicatore di bank segnava circa 15°, molto più dei 7 gradi previsti. Come mai? In effetti c'era qualcosa di strano: per tenere l'aereo su questa orbita dovevo spingere il motore quasi al massimo, sintomo che l'aerodinamica stava funzionando molto male, cioè la virata non era coordinata. In queste condizioni il turn and slip indicator segna una accelerazione laterale consistente, e i miei poveri passeggeri si sentono spinti verso l'interno della curva.
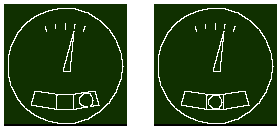
|
A sinistra: situazione dell'indicatore di virata e sbandamento in condizioni di virata scoordinata a destra a 1,5°/s, con forte accelerazione laterale. Notare il tubo ricurvo dello sbandometro: la pallina al suo interno è deviata a destra, ad indicare che c'è un'accelerazione laterale. A destra: virata coordinata. La pallina al centro indica che l'accelerazione è verticale. |
La virata scoordinata è dovuta alla diversa velocità dell'aria sulle ali e alla diversa inclinazione degli alettoni: l'ala esterna alla curva incontra l'aria a maggiore velocità, produce quindi più attrito e tende a fare ruotare il muso dell'aereo verso l'esterno della curva, ponendo il suo asse di traverso rispetto al flusso dell'aria; inoltre l'alettone dell'ala esterna alla curva è piegato in basso e genera più attrito.
Per correggere l'assetto bisogna usare il timone della coda (rudder), in modo da aiutare l'aereo ad eseguire la curva. I tasti che controllano il timone sono z (per virare a sinistra), c (per virare a destra) e x (per riportare il timone in centro). Nel caso della mia virata, ho azionato il timone a sinistra premendo z per ben 22 volte! Effettivamente il controllo del timone è un po' troppo fine...
L'effetto benefico del timone si fa però sentire: il motore passa dall'88% al 66%, mentre l'angolo di bank scende al valore atteso di 7°. Con un angolo di bank di soli 7° la portanza richiesta cresce solo di un fattore 1/cos(7°)=1,01 cioè +1% e quindi si può anche tralasciare di intervenire sul motore. Inoltre l'accelerazione laterare si annulla, e i miei passeggeri sperimentano solo un maggiore "peso" che li schiaccia sui sedili (+1%).
Quindi, in definitiva, ecco le istruzioni per eseguire una virata coordinata a 3°/s:
La virata coordinata ben eseguita praticamente non richiede di regolare il motore. Una volta imparato, la virata coordinata consente di manovrare a velocità più alte e con maggiore precisione.
Sull'aeroplano vero il pilota avverte le accelerazioni laterali e le compensa in modo naturale agendo sul timone, che si comanda con la pedaliera. Nel simulatore tutto questo manca e usare i tasti è poco intuitivo. Per fortuna, nel simulatore così come in molti aeroplani, c'è l'automatismo di autocoordinamento timone/alettoni (AC). Il documento Auto-coordinamento timone/alettoni spiega come usare queste funzionalità.
Il programma è anche in grado di eseguire le virate standard in modo del tutto automatico, ma questo toglie tutto il divertimento.
Alcune procedure di volo delle carte di navigazione impongono di percorrere archi di circonferenza di un determinato raggio. Quali fattori influenzano il raggio dell'orbita? e come fare a calcolare questo raggio?
Il calcolo dell'orbita diventa più facile se premettiamo alcune osservazioni. Indichiamo con r il raggio dell'orbita, che viene percorsa con velocità lineare v e con velocità angolare w (quest'ultima espressa in radianti al secondo, essendo 360° = 2π rad). Queste tre grandezze sono correlate dalla formula
v = r w
Il grafico qui sotto mostra il raggio dell'orbita in funzione della velocità per vari angoli di bak. Ad esempio, una data carta di navigazione potrebbe richiedere di eseguire una virata con un raggio di 2 NM per allinearsi al LOCATOR della pista; se v=180 kt allora l'angolo di bank deve essere di circa 13 gradi (siccome la curva 13° non c'è nel grafico, occorre fare una interpolazione tra la curva dei 10 e quella dei 15).
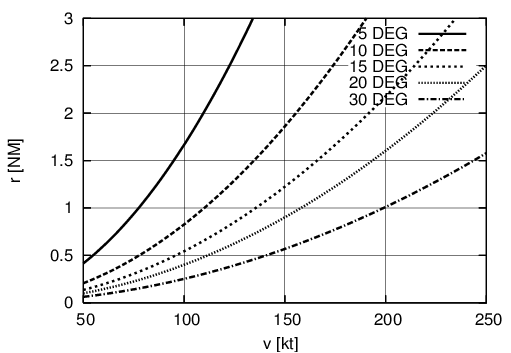
Raggio dell'orbita in funzione della velocità per vari angoli di bank.
Ci tornerà utile calcolare il tempo di percorrenza T di un tratto rettilineo lungo come il raggio della circonferenza. Questo tempo è dato dal rapporto r/v ma, sostituendo r=v/w dato dalla formula precedente, rimane:
T =
1 w
Ad esempio, con w = 3°/s si ha T = 19 secondi. Con una velocità angolare w = 1,5°/s questo tempo raddoppia a 38 secondi.
|
Ricorda che per svolgere i calcoli nelle formule gli angoli vanno sempre espressi in radianti. Questo rende le formule più semplici perché spariscono una quantità di coefficienti che ne oscurerebbero il significato. In altre parole, i radianti sono l'unità di misura più "naturale" dal punto di vista matematico. In pratica, per eseguire i calcoli numerici basta sostituire il simbolo ° = DEG con π/180. Ad esempio 3°/s = 3 π / 180 / s = 0,0523 / s. |
Si possono immaginare diversi tipi di virata. Nel seguito ne consideriamo alcune che possono tornare utili, naturalmente con il proposito di andarle poi a verificare sul simulatore. Ricordiamo che tutti i tratti dell'orbita devono essere percorsi a uguale velocità, e che gli archi di circonferenza sono determinati dall'heading finale da raggiungere (cioè la direzione segnata dalla bussola), mentre i tratti rettilinei sono determinati dai tempi di percorrenza.
Adesso che siamo in grado di eseguire con sicurezza virate standard a 3°/s, ci occorre un modo per verificarle con il simulatore. Come si sà, la teoria è una cosa, ma la pratica (anche se simulata) è un'altra cosa. Un modo semplice è di usare un VOR/DME. Scegliere un VOR/DME, per esempio il solito CVE, che è vicino alla pista di partenza della scena default. Impostare la frequenza sull'HSI e ruotare l'OBS fino a 90°. Salire alla quota di circa 2000 ft e stabilizzare la velocità su v=100 kt a 59% RPM. Fare in modo di tagliare il radiale scelto venendo da sud con true heading TH=0° e a una distanza dal VOR/DME di circa d1=5 NM. Una volta tagliato il radiale (il CDI segna zero), annotare la distanza dal VOR/DME. Proseguire oltre il radiale per una decina di secondi, quindi virare a destra di 180°, drizzare e intercettare di nuovo il radiale. Oltrepassare il radiale e continuare per una decina di secondi, quindi virare a sinistra di 180° e tagliare di nuovo il radiale. Ripetere le manovre come nella figura qui sotto, in modo da tagliare il radiale per 5 volte.
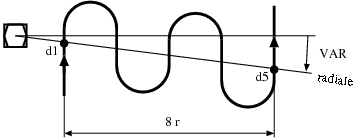
Verifica del raggio di virata.
Annotare la distanza d5 dell'ultimo passaggio sul radiale. I parametri da tenere costanti sono: la quota, la velocità, la velocità di virata. Il raggio medio delle proprie orbite è dato dalla formula:
rm =
d5 − d1 cos(VAR) 8
dove VAR è la variazione magnetica nei pressi del VOR/DME. Il risultato ottenuto dovrebbe coincidere con il valore teorico dato dalla formula pratica:
per virate a 1,5°/s:
r =
v NM 94 per virate a 3°/s:
r =
v NM 188
Per la velocità di 100 kt a 3°/s il raggio teorico è 0,532 NM. Tenuto conto dell'errore di quota (minore di 0,01/8 NM) e dell'errore di lettura del DME (circa 0,1/8 NM), se le nostre manovre fossero perfette il raggio medio ottenuto dovrebbe differire dal raggio teorico per non più di 0,02 NM.
|
Regola per il calcolo mnemonico del raggio di virata. Per eseguire con precisione le manovre è importante avere sempre un'idea del raggio di virata, anche se approssimata. Una regola pratica di calcolo è la seguente: il raggio di virata è la velocità diviso 200 per il rateo di 3°/s; il raggio è la velocità diviso 100 per il rateo di 1,5°/s. Ad esempio a 180 kt il raggio della virata standard è di 0,9 NM. Questa regola di calcolo mnemonico dà un errore del −6% ma è comunque utile. |
In generale senza avvalersi degli automatismi del programma è piuttosto impegnativo mantenere l'aereo su di una virata perfetta, e inevitabilmente ci sono delle oscillazioni in più e in meno. Queste oscillazioni intorno al valore di riferimento non pregiudicano la precisione della manovra perché tendono a compensarsi.
Inutile sforzarsi di mantenere gli indicatori "inchiodati" sul valore di riferimento. Bisogna invece imparare a manovrare con delicatezza facendo piccole correzioni con il mouse, compensando il ritardo nella risposta dovuto all'inerzia dell'aereo. Una volta acquisita una certa esperienza con un dato aereo, risulterà facile trovare il punto di equilibrio giusto in modo che l'aereo segua docilmente i nostri comandi.
Nel seguito passeremo in rassegna alcune manovre tipiche. Le carte di volo in generale riportano i fix point sui quali iniziare le varie manovre, e sono progettate tenendo conto dei criteri che qui descriveremo.
Serve per invertire la rotta e ripassare sul punto iniziale (fix point) mantenendo l'allineamento. Il fix tipicamente è un VOR o un riferimento visivo, per esempio l'estremità della pista sulla quale dovremo atterrare.
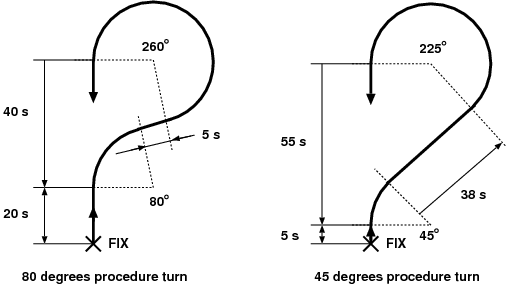
Le virate standard vanno eseguire a un rateo di 3°/s. Al termine della manovra queste procedure lasciano un minuto di tempo per stabilizzare l'aereo prima di ripassare sul fix. Durante le manovre la velocità deve rimanere sempre costante.
L'80 degrees procedure turn prevede di passare il fix e procedere per altri 20 s, quindi virare a destra per 80°, drizzare e procedere per 5 s, quindi virare a sinistra fino a raggiungere di nuovo l'allineamento. Una volta terminata la virata, rimane un minuto di tempo per stabilizzare l'aereo prima di ripassare sul fix. In pratica, il segmento da 5 secondi non si considera, ma si passa semplicemente dalla virata a destra alla virata a sinistra, cosa che richiede comunque qualche secondo.
La 45 degrees procedure turn prevede di proseguire dopo il fix per 5 s, virare a destra di 45°, procedere per 38 s, quindi virare a sinistra per 225° fino a raggiungere di nuovo l'allineamento. Una volta terminata la virata, rimane un minuto di tempo per stabilizzare l'aereo prima di ripassare sul fix. Questa manovra è qualche secondo più lunga della precedente, ma secondo me è meno critica nei tempi, permettendo di ottenere un migliore allineamento finale.
E' possibile ovviamente scambiare le virate destra con sinistra. E' anche possibile eseguire le virate con un rateo di 1,5°/s, ma in questo caso tutti i tempi vanno raddoppiati. Se la manovra a 3°/s non riesce, conviene provare prima con la manovra a 1,5°/s che è più facile.
Applichiamo ancora le formule ottenute ad un'orbita molto semplice che permette di virare di 90° sul fix point. Il fix point in questione potrebbe essere anche l'intersezione con il radiale di un VOR o con l'ILS di una pista: in questi casi la manovra permette di immettersi con precisione sul radiale o sul percorso di discesa.
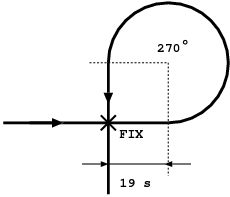
La manovra si descrive così: una volta raggiunto il fix point, proseguire per un tratto pari al raggio (cioè 19 secondi per w=3°/s, 38 secondi per w=1,5°/s) quindi virare per 270° e ripassare sul fix point.
E' facile generalizzare questa manovra per angoli diversi da 90°. Indichiamo con A la variazione di rotta, cioè l'angolo tra la direzione di arrivo e la direzione di allontanamento dal fix point (v. figura qui sotto).
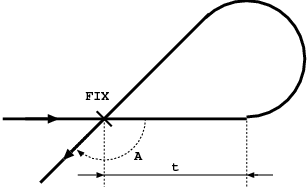
Allora un semplice ragionamento geometrico sull'orbita porta al tempo di percorrenza del tratto rettilineo pari a
t = 19 tan(A / 2) secondi
Ad esempio, per A=90° otteniamo 19 secondi, per A=135° otteniamo 46 secondi. Per virate a 1,5° al secondo il tempo deve essere raddoppiato.
Questa virata si trova spesso nelle carte di atterraggio. Un terminal VOR collocato vicino alla pista fornisce il fix point di riferimento. Siccome a grande distanza il VOR si può considerare coincidente con la pista, l'heading finale della virata è l'heading della pista, mentre l'heading iniziale dipende dalla distanza dalla quale vogliamo iniziare la discesa. Indicata con d la distanza alla quale vogliamo iniziare la discesa, allora l'angolo A deve valere
A = 2 arctan(d / r)
dove r è il raggio della virata. Ad esempio, per d=10 NM e r=0,53 NM si ha A=10°. Di solito si preferisce indicare i tempi, piuttosto che le distanze. In questo caso basta ricordare che r=v tr dove tr è il tempo di percorrenza di un tratto rettilineo pari al raggio della virata (19 secondi per 3°/s e 38 secondi per 1,5 °/s) mentre d=v t. Sostituendo nella formula di prima si ottiene l'angolo di variazione di rotta in funzione del tempo di percorrenza del tratto rettilineo:
A = 2 arctan(t / tr)
Serve per immettersi su di un dato radiale del VOR/DME proveniendo da una direzione arbitraria. E' una manovra tipica richiesta per immettersi sul percorso che conduce verso la pista, oppure che conduce verso il cammino di discesa dell'ILS. Iniziando la virata sopra al VOR/DME (vedi la figura qui sotto a sinistra) non si ottiene il corretto allineamento a causa del raggio dell'orbita della virata. Nella parte destra della figura la virata viene anticipata quando l'aereo si trova a una distanza RV dal VOR/DME.
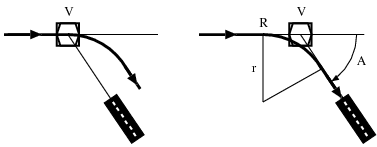
Virata non precisa (a sinistra) e precisa (a destra) sul VOR/DME.
Indicato con A la variazione di rotta senza segno, un semplice ragionamento geometrico porta alla formula che dà l'anticipo con il quale dobbiamo iniziare la virata:
RV = r tan(A / 2)
dove r è il raggio di curvatura delle nostre virate. Ad esempio, se la variazione di rotta è A=90° allora RV=r. La tabellina qui sotto riporta i valori di RV per alcuni angoli notevoli.
| A | RV |
|---|---|
| 20° | 0,2 r |
| 30° | 0,3 r |
| 45° | 0,4 r |
| 60° | 0,6 r |
| 90° | 1,0 r |
E' facile memorizzare la tabella: l'anticipo RV si ottiene dividendo la variazione di rotta per 100 e moltiplicando per il raggio di virata. In altre parole, vale la seguente formula approssimata applicabile mentalmente:
RV = r A / 100
Seguire il radiale di un VOR è la soluzione più semplice e sicura per mantenere la rotta. Prima o poi, però, dovremo abbandonare il radiale per seguire un'altra rotta, che in generale non è il radiale di un VOR. Il problema è: a quale distanza dal VOR/DME bisogna incominciare la virata? Nella figura qui sotto il radiale VP interseca la nuova rotta nel punto P, mentre l'angolo A è la variazione di rotta.
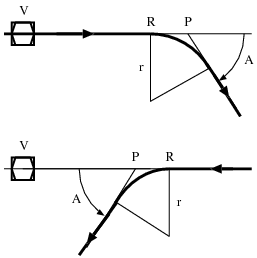
Uscita dal radiale in allontanamento e in avvicinamento al VOR/DME.
Siccome il raggio della virata r non è trascurabile, dovremo anticipare leggermente la virata alla distanza VR dal VOR/DME invece che alla distanza VP. Il problema è calcolare questo anticipo, cioè il segmento RP. Semplici considerazioni geometriche portano alla seguente formula:
RP = r tan(A / 2)
L'angolo A è la variazione della rotta, senza segno. Ad esempio, alla velocità lineare v = 120 kt e alla velocità angolare di virata standard w = 3°/s, il raggio di virata risulta r = v/w = 0,6 NM. Supponiamo che il cambiamento di rotta sia A = 60°. Allora la virata deve essere anticipata di r tan(60°/2) pari a 0,35 NM. Per angoli fino a 90° si può usare la seguente formula approssimata, facile da applicare anche mentalmente:
RP = r A / 100
Sempre coi dati dell'esempio, la formula approssimata avrebbe dato 0,36 invece che 0,35.
E' il problema opposto al precedente: a partire da una rotta arbitraria, immettersi in un dato radiale del VOR/DME. Nella pratica i piloti si basano sulla loro esperienza di pilotaggio, e conducono la manovra osservando il movimento del CDI ed eseguendo qualche correzione di rotta, fino al completo allineamento con il radiale. Qui affrontiamo la questione da un punto di vista geometrico sperando di imparare qualche cosa e sempre con l'obiettivo di andare poi a verificare il tutto sul simulatore.
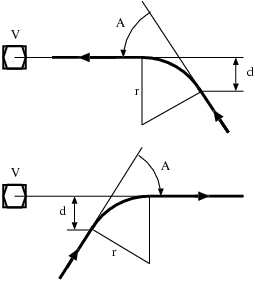
Immissione nel radiale in avvicinamento e in allontanamento dal VOR/DME.
Si vede dalla figura che, se A è la variazione di rotta necessaria per immettersi nel radiale voluto, allora la virata deve iniziare quando d è pari a r (1 − cos(A)). La formula esatta non ha reale interesse perché è piuttosto complicata da applicare mentre si è in volo.
Diamo invece alcune indicazioni pratiche per svolgere il calcolo mentalmente, anche se in modo approssimato. A tal fine ritornano utili le considerazioni fatte nel documento relativo alla navigazione, dove abbiamo detto che ogni pallino del CDI del nostro simulatore corrisponde a 1,7° e che pertanto la distanza lineare d del radiale selezionato si ottiene dividendo la distanza dal VOR/DME per 100 e moltiplicando per tre e quindi moltiplicando per il numero di punti di scostamento segnati dal CDI del nostro HSI. Nella pratica l'angolo di incidenza A varia tra 30° e 90°, per cui possiamo calcolare il valore della distanza per gli angoli notevoli più comuni. Se l'angolo di incidenza è diverso da quelli elencati nella tabella, il pilota si può risparmiare molti calcoli semplicemente portanto l'aereo sull'angolo di incidenza più prossimo a uno dei valori della tabella prima di iniziare la manovra.
| A | d | d [NM] (v=80 kt, 3°/s) |
d [NM] (v=100 kt, 3°/s) |
d [NM] (v=120 kt, 3°/s) |
|---|---|---|---|---|
| 30° | 0,13 r | 0,1 | 0,1 | 0,1 |
| 45° | 0,3 r | 0,1 | 0,2 | 0,2 |
| 90° | r | 0,4 | 0,5 | 0,6 |
Per praticità ho calcolato esplicitamente i valori della distanza per alcune velocità tipiche del nostro aereo da addestramento. Viste le basse velocità, i raggi di virata sono piccoli e spesso trascurabili per angoli di incidenza inferiori a 45°.
Esempio. Stiamo procedendo con TAS=120 knots a una distanza di 8 NM dal VOR/DME, e ci dobbiamo immettere sul radiale con angolo di incidenza A=90°. Determinare il punto in cui iniziare la virata.
Il raggio di curvatura per una virata standard a 3°/s e alla velocità di 120 knots è di 0,6 NM. Dalla tabella precedente risulta che la manovra deve iniziare quando la distanza dal radiale è d=0,6 NM. Dalla formula pratica che dà la distanza da un radiale d = DME / 100 * 3 * CDI, ricaviamo la deviazione:
CDI =
100 d =
100 0,6 NM = 2 punti 3 DME 3 10 NM Quindi inizieremo la virata quando il CDI indicherà 2 punti di scostamento dal radiale scelto. Bisogna notare che man mano che ci avviciniamo al radiale la distanza dal VOR/DME diminuisce e quindi aumenta CDI, sicché dovremo ripetere il calcolo fino a quando l'indicazione del CDI corrisponde a quella del DME. In pratica, dovrebbe bastare eseguire il calcolo una sola volta usando la distanza DME indicata quando il segmento del CDI comincia a muoversi.
Dall'ultimo esempio si traggono due considerazioni che ci danno la distanza minima e massima dal DME entro le quali ha senso eseguire la manovra di precisione che abbiamo proposto. Questo intervallo di distanze, naturalmente, va rapportato alla velocità del mezzo. Per prima notiamo che il CDI ha una escursione massima di 5 punti, per cui esiste una distanza minima dal DME sotto la quale il CDI comincerà a dare l'indicazione quando ormai non avremo più il tempo di eseguire la manovra (4 NM).
La seconda considerazione riguarda la scarsa precisione del CDI, sul quale è difficile apprezzare scostamenti con una precisione superiore al mezzo punto. Ciò comporta che per distanze superiori a circa 20 NM dal DME la virata verrebbe indicata con una deviazione del CDI inferiore a un punto, e quindi in pratica l'immissione nel radiale può avvenire per correzioni successive.
Le manovre di immissione sul radiale descritte nel precedente paragrafo implicavano la conoscenza della distanza dalla stazione VOR/DME. Se la stazione VOR non ha un DME, quella procedura non è possibile perché non possiamo determinare la distanza dal radiale che vogliamo raggiungere. Una possibile soluzione l'abbiamo già vista parlando della virata a 90° sul fix point. La manovra che descriviamo qui è più veloce e funziona sia con un VOR/DME sia con un VOR.
L'idea è di intercettare il radiale (il CDI segna zero) e poi eseguire una serie di virate per correggere la rotta ed inserirsi sul radiale. La manovra risulta più semplice perché non richiede alcun calcolo da parte del pilota, ma richiede più tempo e più spazio. La figura qui sotto illustra due soluzioni: la prima con intercettazione del radiale a 90° e la seconda a 45°.
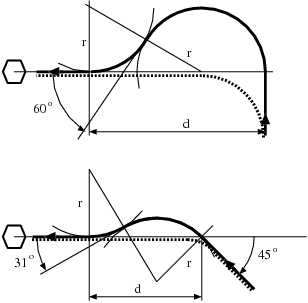
Immissione sul radiale dopo intercettazione a 90° e a 45°.
Intercettando il radiale a 90°, il pilota deve procedere nella direzione perpendicolare al radiale fino a quando il CDI segna zero, quindi deve virare fino a raggiungere la direzione del radiale più 60°, e poi deve virare in senso opposto fino alla direzione del radiale. Alla fine della manovra l'aereo sarà allineato con il radiale. Dal momento della intercettazione del radiale fino al momento in cui raggiunge l'allineamento, l'aereo si sarà avvicinato al VOR di una distanza d=2,7 r, dove r è il raggio della virata. Ad esempio, a 120 kt è r=0,6 NM per cui risulta d=1,6 NM. Per confronto, la linea tratteggiata mostra la manovra di avvicinamento precisa che abbiamo descritto al paragrafo precedente.
Intercettando il radiale a 45°, il pilota deve virare in direzione del radiale più 31°, quindi deve virare in senso opposto fino all'allineamento. In questo caso la distanza percorsa verso il radiale dal momento della intercettazione al momento del raggiunto allineamento è d=2,1 r. Per confronto, la linea tratteggiata mostra la manovra di avvicinamento precisa che abbiamo descritto al paragrafo precedente.
Queste manovre hanno il loro punto critico nel momento in cui si deve invertire bruscamente il verso della virata. Questo passaggio deve avvenire nel più breve tempo possibile, oppure il pilota deve anticipare leggermente dopo aver fatto qualche prova. Ad esempio, io comincio a raddrizzare tre o 4 gradi prima, mentre premo il tasto x per raddrizzare il timone e poi tengo premuto c per virare dall'altra parte.
Abbiamo visto una serie di manovre che possono tornare utili nel volo strumentale. Lo studio geometrico delle orbite ha lo scopo di mostrare quali sono gli spazi di manovra necessari per i vari tipi di virata. In generale conoscere la relazione tra velocità, rateo di virata e raggio di virata permette di eseguire con maggior precisione qualsiasi manovra di virata, accostamento a radiale, avvicinamento alla pista e navigazione in generale. Ad esempio, se ci dobbiamo allineare alla pista da una distanza di sole 5 NM (cosa che può accadere in un atterraggio ILS) probabilmente non avremo molte possibilità di correzione in uno spazio così ristretto, per cui dovremo impostare bene l'avvicinamento oppure ritentare.
Ultima questione: a parte le virate standard, si possono fare virate "non standard"? Certo che sì! La discussione che abbiamo fatto qui riguarda solo le manovre di precisione. Per il resto il pilota può eseguire le virate nel modo che preferisce, purché coordinate. Esiste semmai un limite all'angolo di bank: in una virata coordinata ad ogni angolo di bank corrisponde una accelerazione sperimentata dai passeggeri pari a g/cos(A), dove g è l'accelerazione di gravità.
Ad esempio, con un angolo di bank di 30° l'accelerazione è 1,2 g, ben tollerata dai passeggeri e dalle strutture dell'aereo. Un aereo da caccia può spingersi ad angoli di bank prossimi a 90°, ed in questo caso torna utile l'indicazione dell'accelerometro in alto a sinistra nell'HUD. Ma attenzione, una accelerazione molto forte tra i 6 e gli 8 g si può tollerare solo per qualche istante, poi il sangue nel cervello si sposta inesorabilmente verso le parti basse del corpo, la vista si appanna e si perde conoscenza.
| Umberto Salsi | Commenti | Contatto | Mappa | Home / Indice sezione |
Still no comments to this page. Use the Comments link above to add your contribute.