Home / Indice sezione

www.icosaedro.it

 Quadro delle unità di misura

Ultimo aggiornamento: 2023-04-04

Quadro riassuntivo delle unità di misura e delle equivalenze. Tutti i numeri sono arrotondati a 4 cifre significative, salvo i casi in cui esiste un rapporto esatto tra le due unità.

Indice

Distanze/Lunghezze
Tempi
Velocità
Angoli
Massa
Forza
Pressione
Come si eseguono le conversioni

Distanze/Lunghezze

Miglio nautico

Come spiegheremo nel documento sulla navigazione aeronautica, il miglio nautico ha un significato geometrico semplice: se si percorre un angolo di un primo d'arco lungo un meridiano o sull'equatore, la distanza percorsa è pari a (circa) un miglio nautico. Ecco perché questa unità viene comunemente usata da chi percorre distanze su scala planetaria. Per contro il metro e i Km sono lunghezze stabilite in modo del tutto arbitrario e senza alcun nesso con le dimensioni della Terra.

NM = 1852 m = 1,852 Km = 6076 ft

Feet (Piedi)

I piedi (foot al singolare, feet al plurale) vengono comunemente usati per esprimere l'altitudine e rientrano nella velocità di salita e discesa dell'aereo. Si tratta di una lunghezza stabilita in modo arbitrario e senza alcun nesso con il NM, ma è entrata nell'uso nel mondo aeronautico perché le più grandi industrie del settore sono nate negli USA dove questa unità di lunghezza è di uso comune.

ft = 0,3048 m = 0,0001646 NM

Metri

m = 3,281 ft = 0,0005400 NM

Tempi

Il tempo scandisce le varie fasi dell'attività umana nell'arco della giornata. Il giorno viene quindi scomposto in 24 parti dette ore. Il numero 24 è conveniente perché ha tanti divisori, e quindi permette di suddividere la giornata in tanti modi. Sono infatti divisori di 24 i numeri 2, 3, 4, 6, 8 e 12. Le ore sono poi suddivise in 60 minuti, e a loro volta i minuti sono suddivisi in 60 secondi. La ragione della scelta del numero 60 mi è meno evidente, ma probabilmente ha anch'essa motivi di praticità, essendo anche il 60 un buon numero facilmente divisibile in vari modi.

Secondi

s =	1	min =	1	h
	60		3600

Ore

h = 3600 s = 60 min

Minuti

min = 60 s =	1	h
	60

Velocità

Knots

kt = NM/h = 1,852 Km/h

Mach

Il numero di Mach è il rapporto tra la velocità dell'aria che investe l'aereo v e la velocità del suono c alla quota e alle condizioni atmosferiche correnti. Si tratta quindi di un numero puro, al quale noi metteremo l'unità di misura fittizia "Mach". Pertanto:

v	= n Mach
c

Quando n < 1 si hanno i voli subsonici, mentre per n > 1 si hanno i voli supersonici. La velocità del suono c diminuisce al diminuire della pressione, e quindi il numero di Mach non è una unità di misura assoluta della velocità perché varia con la quota. Ad esempio, al livello del mare la velocità del suono è c = 1220 Km/h mentre a 30'000 ft di quota scende a 1093 Km/h. Il numero di Mach è un parametro importante perché il comportamento aerodinamico dell'aeromobile alle velocità elevate (maggiori di 0,3 Mach) dipende da questo valore più che dalla velocità assoluta.

Feet al minuto

ft/min = fpm = 0,3048 m/min = 0,005080 m/s = 0,0005400 NM/min

Questa unità viene usata per esprimere il rateo di salita o di discesa dell'aereo. Come abbiamo detto, la scelta del ft come unità di lunghezza è piuttosto arbitraria. L'unità di tempo è invece appropriata, siccome le manovre di salita e di discesa avvengono in una scala di tempo dell'ordine dei minuti.

Chilometri all'ora

Km/h = 0,5400 NM/h = 0,5400 kt

Angoli

Radianti

L'unità di misura degli angoli è il radiante, cioè il rapporto tra la lunghezza dell'arco di circonferenza che sottende l'angolo e la lunghezza del raggio della circonferenza stessa. Essendo il rapporto di due lunghezze, ne segue che il radiante è in realtà un numero puro e quindi non richiede unità di misura. Tuttavia per non far confusione si usa sempre indicare gli angoli aggiungendo "RAD" come unità di misura fittizia che vale esattamente 1. Tutte le formule sottintendono che gli angoli siano espressi in radianti.

RAD = 1 = 180/π DEG = 57,30 DEG

Quindi il radiante non è una unità di misura ma è solo un fattore numerico che vale 1.

Gradi

L'angolo giro (cioè l'intera circonferenza) viene suddivisa in 360 parti uguali dette "grado d'arco", o semplicemente "grado" (DEG). Il numero 360 è molto conveniente perché ha tanti divisori che permettono di scomporre variamente gli angoli in parti uguali. Sono infatti divisori di 360 i numeri 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120 e 180. Il grado è quindi l'unità di misura degli angoli umanamente leggibile.

DEG = π/180 RAD = 0,01745 RAD

Quindi il grado non è una unità di misura ma è solo un fattore numerico che vale π/180.

Massa

Chilogrammi

kg = 2,205 lb

Libbre (pounds)

A volte le libbre (in inglese "pounds") vengono scritte nella forma plurale abbreviata "lbs", altre volte "lbs.". Le unità di misura non vanno mai scritte al plurale, né va usata la forma con il punto di troncamento. Perciò si scrive solo "lb" sia che si tratti di una libbra, sia che siano 10.

lb = 0,4536 kg

Slug

Unità di massa "esotica" che corrisponde a una massa che si muove con accelerazione di 1 ft/s² quando le viene applicata una forza di 1 libbra-forza. La discussione delle forze che segue dovrebbe chiarirne il significato. Diamo solo i coefficienti di conversione nelle unità più comuni:

slug = 32,17 lb = 14,59 Kg

Qualche volta gli slug vengono erroneamente usati come unità di forza: in questo caso la forza in questione è il peso della massa di 1 slug misurato sulla Terra al livello del mare.

Forza

Secondo la famosa legge di Newton F=m a, la forza F è quella entità capace di accelerare una massa m con accelerazione a. Pertanto 1 Kg che accelera al rateo di 1 m/s² è sottoposto alla forza di 1 Newton. L'accelerazione che sperimentiamo tutti i giorni è quella di gravità, che al livello del mare vale intorno a a = 9,806 m/s². Questo valore è così comune nei calcoli che viene indicato con la lettera g e la forza che produce ha anche preso un nome specifico: forza peso o anche più brevemente peso. Il peso di 1 Kg è quindi 9,806 Newton.

Ma attenzione: l'accelerazione di gravità varia da punto a punto, perché bisogna tenere conto dell'accelerazione centrifuga (massima all'equatore e nulla ai poli), della non sfericità della Terra (essendo schiacciata, chi sta all'equatore è più lontano dal centro e quindi sente meno la forza di gravità) e della non uniforme distribuzione delle masse all'interno della Terra. Il risultato è che al polo nord pesiamo circa lo 0,7% in più che sulle montagne delle Ande, cioè una differenza di 350 grammi per una persona di 50 Kg: non avvertibile, ma sicuramente misurabile.

Esistono strumenti per misurare il peso che confrontano il peso dell'oggetto da misurare con la compressione di una molla: semplicemente, più l'oggetto è pesante, più la molla si comprime. La compressione della molla aziona un indice su di una scala graduata che indica i Newton. Se lo strumento viene utilizzato alla quota del mare, e i valori della scala vengono divisi per g, allora la bilancia indica direttamente la massa. L'indicazione cambia di poco se si sale su di una montagna, ma le bilance di precisione devono essere corrette anche per il fattore altitudine. Ad esempio 1 Kg di mele pesa 9,806 Newton al livello del mare, ma scende a 9,745 Newton (−0,63%) alla quota di 20 Km alla quale può volare un aeroplano ad alte prestazioni.

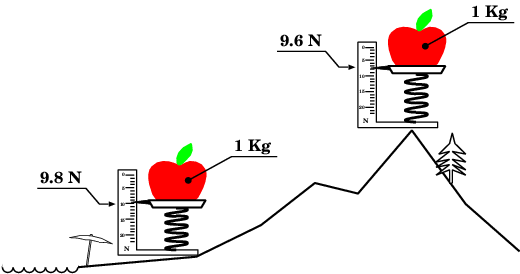
Una massa di 1 Kg di mele pesa 9,8 N al livello del mare. Il peso diminuisce al crescere dell'altitudine per via della maggiore distanza dal centro della Terra, sebbene la massa della merce pesata sia la stessa.

Quindi, mentre la massa è una quantità indipendente dal luogo, la forza peso può variare anche dello 0,7% semplicemente spostandosi sulla Terra. Il problema può interessare un gioielliere, ma non preoccupa un fruttivendolo montanaro e neanche un ingegnere aeronautico. E' per questo che nelle applicazioni pratiche comuni si è generata un po' di confusione tra massa e peso che sono viste come due cose equivalenti, per cui non è raro leggere affermazioni sbagliate come "pesa 10 Kg" oppure "pesa 5 libbre". Per ristabilire un po' di rigore bisognerebbe dire semmai "pesa 10 Kgf" oppure "pesa 5 lbf". Il chilogrammo-forza (Kgf) è una forza pari al peso di 1 Kg misurato sulla Terra al livello del mare. Una libbra-forza (lbf) è il peso di una libbra misurato sulla Terra al livello del mare. Negli USA libbre e libbre-forza vengono di solito confusi e considerati sinonimi, esattamente come da noi il chilogrammo e il chilogrammo-forza, per cui non è raro trovare anche nella documentazione tecnica questo genere di equivoco.

Pertanto le formule di conversione sono queste:

g = 9,806 m/s² = 32,17 ft/s²

Kgf = 1 Kg g = 9,806 N = 2,205 lbf

lbf = 1 lb g = 32,17 lb ft/s² = 4,448 N = 0,4536 Kgf

N = 1 Kg m/s² = 0,1020 Kgf = 0,2248 lbf

Ad esempio, un motore a getto che sviluppa una forza di spinta di 10'000 N equivale a 1020 Kgf ovvero 2248 lbf. Se applichiamo questo motore a un aeroplano a decollo verticale e lo facciamo funzionare al livello del mare, potremo sollevare una massa fino a 1020 Kg, ovvero 2248 libbre. La massa in questione include il carburante e il motore stesso, naturalmente. E' più conveniente applicare questo motore a un aereo con le ali, e allora potremo far volare un peso molto maggiore. Ad esempio, il Boeing 747-400 a pieno carico pesa circa 3'500'000 N e i suoi motori generano al livello del mare una spinta massima di "soli" 890'000 N, ma più che sufficienti per farlo alzare da terra.

Nel documento Le forze che agiscono sull'aereo vedremo che la spinta minima che deve produrre il motore di un aeroplano ad ala fissa per mantenerlo in volo dipende dal suo rapporto lift/drag (L/D). Per i piccoli aerei da turismo il rapporto L/D vale circa 10, che significa che la spinta deve essere almeno pari a 1/10 del peso; per gli aerei di linea il rapporto L/D può salire a 17, perciò la spinta minima sarà 1/17 del peso. Questo dimostra quanto sia più vantaggioso un aereo ad ala fissa rispetto a un aereo a decollo verticale come un elicottero.

Pressione

Per la regolazione dell'altimetro bisogna impostare la pressione della isobara di riferimento rispetto alla quale lo strumento indicata l'altezza. Si hanno quindi i diversi tipi di regolazioni convenzionali denominate QNH, QNE e QFE a seconda che la pressione della isobara di riferimento impostata sia rispettivamente quella al livello del mare, quella di 29,92 pollici di mercurio (inchHg), oppure quella dell'areoporto. Siccome il METAR fornisce il QNH in hecto-Pascal (hPa = 100 Pa), e siccome alcuni altimetri riportano solo la scala in pollici, sorge la necessità di convertire gli hPa in inchHg, tenendo presente che 1013 hPa = 29,92 inchHg:

hPa = 1 millibar = 0,02954 inchHg

inchHg = 33,86 hPa

Per completezza ricordiamo anche che, per definizione, 1 Pa = 1 N/m² e che 1 inchHg è la pressione esercitata dal peso di una colonna di mercurio alta 1 pollice e posta al livello del mare e al di sopra della quale c'è il vuoto.

Come si eseguono le conversioni

Nel mondo internazionale dell'aeronautica capita di trovare valori espressi nelle combinazioni più strane, per cui sorge la necessità di convertirli nelle unità a noi più familiari, basta sostituire le unità "indesiderate" con il loro equivalente riportato qui e poi eseguire i calcoli che coinvolgono i numeri rimanenti.

Ricordare di proseguire il calcolo indicando sempre l'unità di misura al fianco dei numeri. Se, alla fine del calcolo, risulta un valore sbagliato dimensionalmente, allora avremo la prova che abbiamo sbagliato il calcolo o abbiamo sbagliato formula. Insomma, una specie di prova del 9 per le unità di misura.

Ricordare inoltre che le unità di misura vanno considerate come costanti positive ignote. Quindi ad esempio, m*m=m², Kg/Kg=1. Alcune unità di misura sono fittizie perché sono esse stesse dei rapporti di quantità dimensionalmente uguali, e quindi sono numeri puri: esempi di questo tipo sono Mach, RAD e DEG.

Ad esempio: un aereo col motore bloccato precipita da una altezza sul terreno di 5000 ft al rateo costante di discesa di 1200 ft/min; dopo quanti secondi si schianta? Il tempo richiesto è dato dalla solita formula SPAZIO/VELOCITA':

5000 ft	=	5000 ft min	=	5000 60 s	= 250 s
1200  ft   min		1200 ft		1200

Altro esempio: un aereo che viaggia alla velocità v = 100 kt esegue una virata standard al rateo di w = 3 DEG/s; calcolare il raggio dell'orbita espresso in Km. Come vedremo nel documento dedicato alle virate standard, il raggio dell'orbita è dato dalla formula:

r =	v
	w

Sostituiamo ai simboli della formula i rispettivi valori dati dal problema, avendo sempre cura di indicare anche le unità di misura insieme ai numeri. Poi usiamo le equivalenze tra le unità di misura per sostituire le unità indesiderate con quelle volute. Vediamo come procede la conversione:

=	100 kt	=	100 kt s	=	100 1,852 Km s	= 0,98 Km/RAD
	3  DEG   s		3 DEG		3600 s 3 0,01745 RAD

dove il RAD d'avanzo si può ignorare perché vale 1. Il raggio dell'orbita cercato è pertanto di 0,98 Km.

Still no comments to this page. Use the Comments link above to add your contribute.