Home / Indice sezione

www.icosaedro.it

 Le forze che agiscono sull'aereo

Ultimo aggiornamento: 2008-07-27

Indice

Le forze che agiscono sull'aeroplano
Calcolo del lift e del drag
Coefficienti di lift e drag
Velocità di stallo
Il flusso d'aria genera il lift e il drag
Le forze per il C-172RG
Le forze per l'MD-81

Le forze che agiscono sull'aeroplano

Nel seguito supporremo l'aereo in volo livellato a velocità costante, per cui la verticale è quella geodetica. La figura qui sotto mostra le tre forze che agiscono sul centro di massa dell'aeroplano:

• Il peso m*g, dove m è la massa e g è l'accelerazione di gravità.
• La spinta T del motore (Thrust), che supponiamo sia sempre allineata con l'asse x dell'aeroplano.
• La forza aerodinamica totale F, che si scompone nella componente verticale L (Lift o portanza) e nella componente orizzontale D (Drag o attrito).

L'asse longitudinale x dell'aereo è inclinato di un certo angolo A rispetto al flusso dell'aria, e viene detto angolo di attacco.

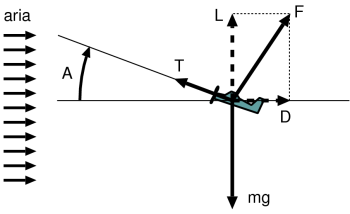
Le forze che agiscono sull'aeroplano.

L'aeroplano non cade perché il peso viene bilanciato dalla componente L della forza aerodinamica sommata alla componente verticale T*sin(A) della spinta prodotta dal motore. Inoltre la velocità si mantiene costante perché l'attrito D viene bilanciato dalla componente orizzontale T*cos(A) della spinta del motore.

Calcolo del lift e del drag

Lift e drag sono dati dalle seguenti formule fenomenologiche:

L = 0.5 rho WingArea V² C_L(A,flap)

D = 0.5 rho WingArea V² C_D(A,flap)

• rho = 1,225 Kg/m³ = 0,07648 lb/ft³ è la densità dell'aria standard al livello del mare. Ovviamente alle quote più elevate la densità cala, perciò i valori calcolati dipendono dalla quota a cui ci si riferisce.
• WingArea è la superficie equivalente dell'aeroplano considerato come un'ala. Questo è il valore riportato nelle caratteristiche di base di ogni aeroplano e lo si può stimare grossolanamente come l'area della sagoma dell'aereo visto dall'alto.
• V è la velocità del flusso d'aria che investe l'aereo. Il suo valore deve essere elevato al quadrato, cioè piccole variazioni di velocità producono grandi variazioni della forza aerodinamica. Ad esempio, raddoppiando la velocità, quadruplica la forza aerodinamica (ovviamente a parità degli altri fattori).
• C_L(A,flap) e C_D(A,flap) sono rispettivamente il coefficiente di lift e il coefficiente di drag. Si tratta di numeri puri dipendenti dall'angolo di attacco A e dall'angolo di inclinazione dei flap. Questi numeri dipendono dalla forma dell'aereo.

Coefficienti di lift e drag

L'andamento tipico dei coefficienti C_L e C_D al variare dell'angolo di attacco viene illustrato dalla figura qui sotto:

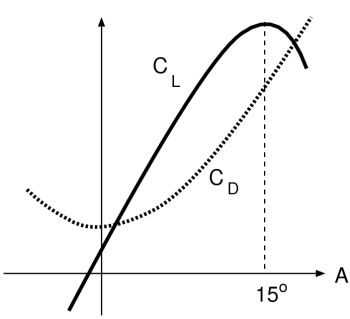
Andamento dei coefficienti di lift e drag al variare di A.

Il coefficiente di lift C_L (linea continua) ha un andamento lineare per un ampio intervallo di angoli di attacco che vanno da circa −2° fino a +15°. Intorno a +15° il coefficiente di lift assume il suo valore massimo.

Nell'intervallo compreso tipicamente tra 14 e 17 gradi di angolo di attacco, il flusso d'aria che passa sopra le ali non riesce più a seguire il profilo dell'ala e diventa turbolento, causando il repentino calo di C_L: in questa condizione si dice che l'aereo è in stallo e incomincia a precipitare.

Il coefficiente di drag C_D (linea tratteggiata) ha un minimo intorno all'angolo di attacco nullo, e cresce rapidamente al crescere dell'angolo di attacco.

In ACM-5.0-ico i coefficienti di lift e drag come funzioni dell'angolo di attacco sono riportati in apposite tabelle di nome CLift e CDrag. Le tabelle riportano i valori per alcuni angoli, mentre per gli angoli intermedi il programma procede per interpolazione.

Quando i flap sono abbassati i coefficienti di lift e drag crescono di una quantità che dipende da quanto sono abbassati i flap. Il programma usa questa formula:

C_L(A,flap) = interpola(CLift,A) + CFlap * sin(flap)

cioè viene interpolata la tabella CLift per il dato angolo di attacco, e poi viene sommato un termine dipendente dall'angolo dei flap e da un coefficiente CFlap anch'esso riportato nelle caratteristiche dell'aeroplano.

Ad esempio, per il C-172RG simulato dal programma, la tabella CLift ha un massimo di 1,65 per A=15°, angolo di attacco al quale comincia anche lo stallo.

Siccome CFlap=1,47 e l'angolo massimo di estensione dei flap è MaxFlap=30°, il coefficiente di lift massimo per questo aeroplano con flap completamente abbassati è max(C_L)=2,385.

Velocità di stallo

La velocità di stallo di un aeroplano dipende dal peso dell'aereo, dalla quota, dall'angolo di deflessione dei flap e dal contributo del motore.

Se lo stallo si verifica ad alta quota, il pilota non deve fare altro che lasciare cadere l'aereo e portare il motore al massimo: una volta riacquistata velocità, il pilota può richiamare il volantino e riprendere quota regolarmente. Il fenomeno comporta solo uno spavento per i passeggeri, ma nessun pericolo reale.

Ben diverso è il caso quando lo stallo avviene a bassa quota: in questo caso l'aereo sbatte violentemente al suolo prima di aver riacquistato sufficiente velocità e prima che il motore abbia ripreso potenza. Di conseguenza le velocità di stallo che interessano sono quelle calcolate a bassa quota.

Si aggiunge poi la condizione peggiore di massimo carico di carburante e massimo carico trasportato (passeggeri, bagaglio e merci).

Si perviene quindi a due velocità di stallo importanti: la velocità di stallo senza flap a motore spento V_s1 e la velocità di stallo con flap a motore spento V_s0. Le formule analitiche per calcolare queste velocità si ricavano dalla formula del lift imponendo che il lift sia uguale al peso dell'aeroplano, cioè L=mg:

V_s = sqrt( 2 m g / (rho WingArea C_L(15°,flap)) )

dove m è la massa massima, g = 9,806 m/s² = 32,17 ft/s² è l'accelerazione di gravità e C_L(15°,flap) è il coefficiente di lift calcolato all'angolo critico di stallo (qui 15°) e con la data regolazione dei flap. Per il C-172RG abbiamo visto che:

C_L(15°,0°) = 1,65

C_L(15°,30°) = 2,385

Essendo la massa massima del C-172RG m=2650 lb, si ottengono le velocità di stallo senza flap e full-flap:

V_s1 = 52,2 kt = 50 KIAS

V_s0 = 43,4 kt = 42 KIAS

che sono esattamente i valori dichiarati dal costruttore. La velocità KIAS è quella riportata dall'anemometro: infatti a causa della inclinazione di un angolo di 15 gradi del tubo Pitot, lo strumento indica solo la componente di velocità dell'aria che è parallela al tubo, che è minore di un fattore cos(15°) rispetto alla velocità reale dell'aria che investe l'aeroplano. Il valore KIAS (knots indicated airspeed) è il numero indicato dal nostro anemometro.

Se il motore è acceso, la componente T*sin(A) della spinta contribuisce al lift, sicché la velocità di stallo diminuisce un po'. Calcolare questo contributo è un po' più intricato perché bisogna calcolare anche il drag. Possiamo invece calcolare il contributo massimo del motore al sostentamento dell'aeroplano supponendo che il motore sia posto alla massima potenza. Per il C-172RG la spinta massima è T_max=270 lbf e la componente verticale di questa forza quando l'aereo è in stallo è T_max*sin(15°) = 70 lbf. L'effetto è quello di ridurre la massa dell'aeroplano di 70 lb appena, cosa che abbassa di poco la velocità di stallo.

Dunque nel caso del C-172RG il motore è così poco potente che il contributo del motore al sostentamento è trascurabile, e le velocità che abbiamo calcolato si possono considerare comunque valide sia con che senza motore. Il pilota deve quindi stare bene attento a non scendere mai sotto questi limiti, soprattutto durante le manovre di decollo e di atterraggio.

Il flusso d'aria genera il lift e il drag

Abbiamo detto che l'aereo viene sostenuto in aria dalla forza di lift, e che questa forza è il risultato della reazione prodotta dal flusso d'aria deviato verso il basso. Cominciamo quindi a calcolare quanto vale questo flusso d'aria. La figura qui in basso mostra un flusso d'aria che procede verso destra con velocità v. Dopo avere incontrato le strutture dell'aeroplano, il flusso d'aria si ritrova deviato verso il basso di un angolo A. Noi supporremo che il flusso deviato conservi la stessa velocità e inoltre trascureremo l'energia dissipata dai vortici e dall'attrito dell'aria contro la superficie dell'aereo.

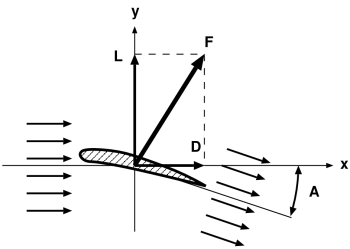
Il flusso d'aria deviato dall'aeroplano. Qui ho riprodotto solo la sezione dell'ala, ma resta sottinteso che dobbiamo considerare l'intera struttura dell'aeroplano. I versi degli assi non sono quelli convenzionali ma ritornano utili per questa discussione.

Consideriamo una certa massa d'aria "da" che viene deviata di un angolo A. Osservando la figura, le quantità di moto prima e dopo la deviazione sono:

q_prima = v da (1, 0)

q_dopo = v da (cos A, −sin A)

La variazione di quantità di moto è la differenza:

dq = q_dopo − q_prima

Dividendo la variazione di quantità di moto per un certo intervallo di tempo dt e cambiando di segno, si ottiene la forza aerodinamica totale che agisce sull'aereo:

F = − dq / dt = v I (1 − cos A, sin A) = (D, L)

dove I è il flusso d'aria I=da/dt cioè quanti Kg di aria vengono deviati dall'aereo ogni secondo. La componente orizzontale è il drag, mentre la componente verticale è il lift. Scritti esplicitamente, il lift e il drag valgono:

L = v I sin A

D = v I (1 − cos A)

Siccome gli angoli A sono piccoli, in genere minori di 10°, conviene approssimare queste formule ponendo sin A = A e ponendo cos A = 1 − 0,5*A². Le formule approssimate che rimangono sono molto semplici:

L = v I A

D = 0,5 v I A²

Ora abbiamo tutte le formule che ci servono. Le applicheremo a due modelli di aeroplano molto diversi, il C-172RG e l'MD-81.

Le forze per il C-172RG

Il miglior rapporto L/D per il C-172RG abbiamo visto essere 14 con v=70 kt per cui l'angolo di deviazione del flusso d'aria è

A = 2 D / L = 0,143 RAD = 8°

Siccome il lift deve bilanciare il peso, cioè L=m g, e siccome m = 700 Kg, possiamo calcolare il flusso dell'aria deviata verso il basso:

I = L / (v A) = m g / (v A) = 1330 Kg/s

Il drag è:

D = 0,5 L A = 0,5 m g A = 490 N

Il motore di un aeroplano in generale produce una spinta che non è esattamente allineata con il flusso d'aria. Pertanto la spinta del motore contribuisce principalmente a contrastare il drag, ma può contribuire anche un po' al lift. Per fare la nostra stima non ci preoccupiamo di questo dettaglio e possiamo considerare questi 490 N come la spinta che il motore del C-172RG deve produrre per mantenere l'aeroplano in volo livellato alla velocità di 70 kt.

Le forze per l'MD-81

Un tipico aereo di linea medio-grande come l'MD-81 ha un best glide ratio superiore a quello del C-172RG di valore tipico intorno a L/D=18 con velocità intorno a 220 kt. Prendiamo per buoni questi valori anche per l'MD-81 simulato dal nostro programma, e vediamo come vanno le cose. L'angolo di deviazione del flusso d'aria risulta essere

A = 0,111 RAD = 6°

La massa dell'MD-81 con 2000 Kg di carburante è m=37000 Kg, per cui il flusso d'aria deviato deve essere

I = 28800 Kg/s

Riflettiamo un attimo su questo numero: si tratta di 29 tonnellate d'aria deviate verso il basso ogni secondo. Un aereo leggero che accidentalmente finisse in questa scia verrebbe destabilizzato dalla turbolenza e spinto violentemente verso il basso.

Veniamo ora alla spinta del motore. Il drag è

D = 20160 N

Siccome la spinta massima dei motori dell'MD-81 è 37000 N al livello del mare, l'aereo può mantenere agevolmente l'andatura di 220 kt ma può anche accelerare con decisione. Ho provato anche a verificare con il simulatore questo valore, facendo stampare la spinta del motore con l'aereo in volo livellato a 2500 ft a 220 kt. Il simulatore fornisce il valore di 22010 N, in buon accordo con la stima ottenuta dalle nostre formule.