
| Home / Indice sezione | www.icosaedro.it |  |
 Il problema del vento
Il problema del ventoLa mia versione modificata di ACM supporta l'impostazione della condizione del vento, che permette di confrontarsi con tutta una serie di problemi di pilotaggio interessanti: il decollo, la navigazione e l'atterraggio.
L'opzione -wind WD/WV del programma permette di impostare
le condizioni del vento espresse come wind direction (WD, gradi)
e wind velocity (WV, knot). Per esempio acm -wind 90/10
è un vento proveniente da est a 10 knots. Il vento simulato dal
programma è costante nel tempo e uniforme a tutte le quote. Nella
realtà le cose sono più complicate, e compensare le
deviazioni causate dal vento richiede abilità ed esperienza,
insieme a qualche semplice considerazione teorica che adesso vedremo.
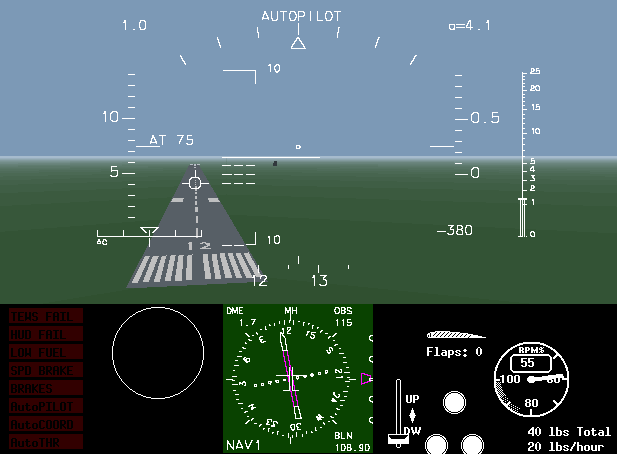
| Figura 1. Atterraggio del C-172 con vento proveniente da destra a 15 kt. Per mantenere il giusto percorso di discesa indicato dal LOCATOR la prora è deviata a destra di circa 10°. Poco prima di toccare la pista dovremo "drizzare" per allineare il carrello e le ruote con l'asse della pista. |
In condizioni normali di volo, l'aria scorre sempre diretta come l'asse longitudinale dell'aereo, in modo che la resistenza sia minima e la portanza sia massima. Se l'aereo prendesse il flusso d'aria di lato anche per pochi gradi, la resistenza opposta sarebbe elevatissima, con conseguente perdita di velocità. Pertanto quando si dice che l'aereo viaggia con un vento "di lato" in realtà il flusso d'aria è sempre diretto come l'asse longitudinale, ma l'aereo subisce una deriva perché trascinato dal vento. Ne consegue che la direzione vera verso la quale stiamo viaggiando non è più quella verso la quale è diretta la prora. Nel seguito determineremo l'entità di questa deviazione e vedremo come compensarla.
L'aerodinamica dell'aeroplano dipende dalla sua velocità rispetto all'aria circostante. A sua volta l'aria si muove rispetto al terreno. Risulta conveniente scomporre la velocità V dell'aereo rispetto a terra in due componenti: la velocità del vento W rispetto a terra e la velocità dell'aereo rispetto all'aria U. La velocità dell'aereo rispetto a terra è quindi la somma vettoriale di queste due componenti:
V = W + Udove
W (wind) è la velocità del vento rispetto al terreno. Il modulo di questo vettore WV (wind velocity) è la forza del vento espressa in kt, mentre l'orientamento WD (wind direction) è la direzione dalla quale spira il vento ed è espressa come direzione geografica in gradi.
U è la velocità dell'aereo rispetto all'aria circostante. Il modulo è la velocità indicata dall'anemometro TAS (true air speed). Questo vettore è diretto come l'asse lungitudinae dell'aereo, cioè la prora TH (true heading).
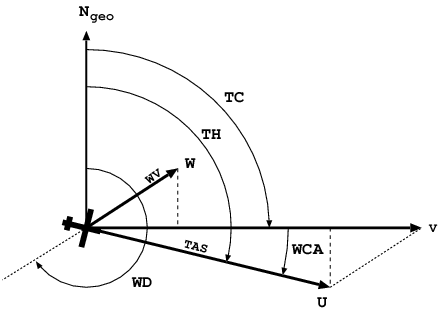
| Figura 2. Il "triangolo del vento" determinato dai vettori velocità del vento rispetto al suolo (W) e velocità dell'aereo rispetto all'aria circostante (U). La risultante V è la velocità dell'aereo rispetto al suolo. |
E' bene chiarire il significato della wind direction (WD), la direzione dalla quale risulta spirare il vento. Per esempio, se il vento proviene da est, allora WD=90°. Il vettore W, invece, è orientato verso west, cioè come WD+180°. Bisogna ricordare questo particolare quando andremo a scrivere le formule, altrimenti rischiamo un errore di 180°! La wind velocity (WV) è la velocità del vento rispetto a terra espressa in knots (NM/h).
La somma dei vettori W e U dà la velocità V dell'aereo rispetto a terra. La direzione di questo vettore è il true course (TC), cioè la direzione nella quale l'aereo sta effettivamente andando. In generale vogliamo che il TC corrisponda alla rotta prevista. Ne consegue che il TH (la direzione verso la quale dobbiamo puntare la prora dell'aereo) differisce di una quantità che si chiama wind correction angle:
WCA = TH − TC
In altre parole, il WCA è la correzione di prora da apportare per compensare il vento, ed è il valore che dobbiamo calcolare. Osservando la figura 2, si nota che la deviazione dell'aereo rispetto al true course è dovuta alla componente trasversale della velocità rispetto al true course, cioè (vedi segmento tratteggiato di sopra)
WV sin( TC − WD + 180° )
Per compensare il vento trasversale, la velocità V deve produrre una componente trasversale uguale in modulo ma di verso opposto (vedi segmento tratteggiato di sotto)
TAS sin( WCA )
L'uguaglianza di questi due termini porta alla formula voluta che dà l'angolo di correzione di rotta:
WCA = arcsin(
WV sin( TC − WD + 180° ) ) TAS
NOTA: in questa formula la funzione arcsin(x) deve dare angoli negativi quando l'argomento è negativo.
A causa del WCA, la velocità con la quale ci avviciniamo alla meta non è il TAS, ma TAS cos(WCA).
Esempio 1. Dobbiamo atterrare con il nostro Cessna 172RG sull'aeroporto di Bologna - G. Marconi pista 12 con un vento proveniente da destra di 15 kt. La situazione vista dal pilota è quella mostrata nella figura 1 all'inizo di questa pagina. Determinare l'angolo di correzione di rotta necessario per mantenere il percorso di discesa indicato dal LOCATOR.
La velocità di atterraggio è TAS=75 kt. L'orientamento della pista è il true course che dobbiamo mantenere TC=115° mentre la direzione del vento è WD=TC+90°=205°. L'angolo di correzione di rotta è
WCA = arcsin(
15 sin( 115 − 205 + 180 ) ) = 11° 75 Calcoliamo il magnetic heading corrispondente, sapendo che la variazione magnetica nella zona è VAR=1°E=+1°:
MH = TH + VAR = TC + WCA + VAR = 115 + 11 + 1 = 127°
Notare che il MH ottenuto corrisponde perfettamente alla prora magnetica indicata dalla bussola (vedi la figura 1): in queste condizioni l'indicatore di percorso di volo inerziale nell'HUD indica che l'aereo sta effettivamente viaggiando verso la pista.
Esempio 2. Si vuole seguire la rotta TC=180° con TAS=120 knots in presenza di vento a WV=15 knots proveniente da WD=130°. Calcolare il true heading TH e la velocità effettiva di avvicinamento alla meta.
Il WCA è:
WCA = arcsin(
15 sin( 180 − 130 + 180 ) ) = −6° 120 Il true heading è TH = TC + WCA = 180 − 6 = 174° mentre la velocità effettiva di avvicinamento alla meta è TAS cos(−6) = 119 knots.
Gli aerei più sofisticati dispongono di un computer collegato alla piattaforma inerziale e all'anemometro che esegue in modo automatico tutti i calcoli del vento e dà al pilota le informazioni sulla correzione di rotta necessaria. Sugli aeroplani che non dispongono di questa strumentazione è evidente che il pilota non può stare a fare tutti questi calcoli, per cui sono stati escogitati sistemi più pratici basati su grafici, tabelle o regoli del vento il cui uso viene descritto nei rispettivi manuali.
Nel nostro caso, ACM presenta l'HUD per tutti i modelli di aereo simulati, incluso il C-172. L'HUD mostra un orizzonte artificiale e il pallino con crocetta che indica la direzione effettiva del moto (il flight path marker). Sfruttando questo ausilio diventa fin troppo facile pilotare nella giusta direzione anche in presenza di vento, soprattutto in fase di atterraggio.
| Umberto Salsi | Commenti | Contatto | Mappa | Home / Indice sezione |
Still no comments to this page. Use the Comments link above to add your contribute.