
| Home / Indice sezione | www.icosaedro.it |  |
 Cartografia aeronautica
Cartografia aeronauticaUna carta nautica accurata è lo strumento primario per pianificare il volo. Qui vediamo come sia possibile rendere sulla carta la complessa forma della superficie terrestre. Vedremo in particolare la proiezione detta di Lambert utilizzata nella cartografia aeronautica.
Le nozioni e le formule che descrivo qui sono quelle che ho usato per generare
le carte di volo distribuite con il programma ACM. Un piccolo
programma che ho scritto legge un file di scenario *.acmscene
e quindi riproduce i dati in esso contenuti; opportuni parametri passati
al programma permettono di definire la scala e il centro dell'area di
interesse. Oltre alle piste, anche le stazioni ILS e VOR vengono riprodotte.
Ovviamente non si tratta di carte "professionali", ma sufficienti per
imparare i primi rudimenti della navigazione e per tracciare le proprie
rotte sugli scenari distribuiti con il programma. Sono disponibili in rete
Internet alcune carte di volo più realistiche che si possono usare in
sostituzione a quelle fornite con il mio programma.
La Terra non è rotonda
La proiezione di Lambert
La scala nella proiezione di Lambert
Costruiamo una proiezione di Lambert
Convenzione ICAO sulle carte aeronautiche
Tipi di carte aeronautiche
Simbologia delle carte aeronautiche
Riferimenti
Effettivamente, il nostro pianeta non è sferico. Una superficie matematica semplice che meglio approssima la superficie terrestre è l'elissoide, ma neppure questo combacia bene. Senza poi contare che la superficie della Terra è scabra, con valli e monti. Se poi decidiamo di rappresentare la superficie della Terra su di un foglio piano, il problema non è risolvibile a meno di accettare qualche approssimazione. Nel seguito di questo documento non ci cureremo della forma esatta della Terra, e assumeremo che le coordinate di longitudine e latitudine di ogni luogo di interesse siano date e siano riferite a una sfera perfetta. Ci occuperemo invece del problema della rappresentazione della superficie sferica sulla superficie piana di un foglio, problema noto col nome di proiezione. In sintesi, si tratta di ottenere una rappresentazione piana che preservi al meglio le distanze e gli angoli. Ciò è essenziale per poter tracciare con precisione le rotte da seguire.
Il tipo di proiezione più usato in ambito nautico e aeronautico è quella inventata dal matematico e filosofo J. H. Lambert nel '700. Nella carta di Lambert, la longitudine lon e la latitudine lat di un punto vengono trasformate nelle coordinate polari r e w secondo queste formule:
r = R ( tan(45° −
lat ) )k 2 w = k lon
dove il parametro R va fissato in modo arbitrario e determina la scala della carta, mentre k è dato dalla formula seguente:
k =
log cos lat1 − log cos lat2
log tan(45° −
lat1 ) − log tan(45° −
lat2 ) 2 2
Infine, lat1 e lat2, detti paralleli standard, sono due latitudini nell'intorno delle quali si vuole eseguire la proiezione. Le deformazioni sulla carta così ottenuta sono tanto più grandi quanto più distanti sono tra loro queste due latitudini, e quanto più ci si sposta lontano da esse sulla carta.
Sappiamo che un primo d'arco sul meridiano equivale a 1 NM, per cui la scala si può ricavare come derivata di r rispetto a lat, ottenendo:
scala =
dr = k R
( tan(45° −
lat ) )k 2 dlat cos lat
Osserviamo che la scala dipende dalla latitudine. La stessa formula permette di calcolare l'andamento delle deformazioni in funzione della latitudine.
Per quanto riguarda la scala complessiva della carta, possiamo usare il valore dato da questa formula in corrispondenza del parallelo standard (uno dei due).
La formula si presta ad essere usata per calcolare R una volta data la scala. Ad esempio, per ottenere una scala di 1:1000000 dobbiamo scegliere R in modo che un miglio nautico di latitudine (dlat = 1' = 0.2909 10-3 rad) venga trasformato sulla carta in un segmento lungo dr = 1852 m / 1000000 = 1,852 mm; il rapporto tra questi due valori dà la scala = 1,852 mm / (0.2909 10-3) = 6366 mm da cui il raggio R.
Per l'area dell'Italia possiamo scegliere i paralleli standard
lat1 = 38°Nlat2 = 46°N
da cui si ricava
k = 0.6697
La proiezione di Lambert posiziona il meridiano zero al centro del settore angolare. Nel nostro caso vogliamo riprodurre solo l'area che ci interessa, per cui centriamo la proiezione rispetto al meridiano di longitudine
lon0 = 12°E
Scegliamo poi la scala 1:500'000, che cioè riduce un primo d'arco dlat=1'=0.2909 10−3 rad (ovvero 1 NM = 1852 m) in dr=3.704 mm. Il valore di R lo calcoliamo dalla formula della scala usando la latitudine standard lat1:
R =
dr cos(lat1) = 24232 mm dlat k (tan(45° − lat1/2))k
Fissiamo sul foglio un sistema di assi cartesiani con l'origine in basso a sinistra, e indichiamo con (x,y) le coordinate di un punto sul foglio largo L. Infine, definiamo una trasformazione dalle coordinate geografiche (lon,lat) di un punto generico alle coordinate del foglio (v. figura):
x = L / 2 + r (lat) sin( k (lon − lon0) )y = r (lat1) − r (lat) cos( k (lon − lon0) )
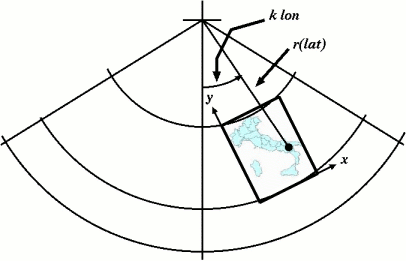
| Trasformazione dalle coordinate polari di Lambert a quelle cartesiane del foglio. L'immagine, ovviamente, non è in scala, altrimenti il polo nord sarebbe dalle parti di Berlino... |
La convenzione ICAO (l'ente internazionale per l'aviazione civile) stabilisce che le carte aeronautiche vengano costruite per fasce di latitudine di 4°. All'interno di questa fascia, lat1 viene collocato 40 primi d'arco più a nord del parallelo sud della fascia, mentre lat2 viene collocato 40 primi d'arco più a sud del parallelo nord della fascia. La scala standard è 1:1'000'000.
Nell'esempio di prima abbiamo invece usato una fascia larga 8° e non abbiamo apportato la correzione di 40' alle latitudini standard; abbiamo usato una scala più ridotta; inoltre il foglio che abbiamo ottenuto è molto grande, e probabilmente andrebbe suddiviso in tante carte più piccole e maneggevoli.
Esistono diversi tipi di carte aeronautiche che differiscono per l'uso VFR (volo visuale) o IFR (volo strumentale), per la scala, per le informazioni di navigazione e comunicazione via radio, ecc.
Le Enroute Charts mostrano le aerovie che collegano i vari aeroporti, inclusi i fix points e i radio fari NDB e VOR. La scala tipica è 1:1'000'000.
La SID (Standard Instrumental Departure) mostra le modalità per il decollo da una data pista, incluse le manovre per aggirare gli ostacoli e le aree abitate, e le manovre da eseguirsi per immettersi nelle aerovie verso le varie destinazioni. La carta può includere sia un diagramma a piccola scala con le rotte da seguire, sia una descrizione in prosa.
La carta STAR (Standard Terminal Arrival Chart) mostra la procedura IFR da eseguire per abbandonare una aerovia e immettersi sulla pista di un dato aeroporto.
La carta IAP (Instrumental Approch Procedure) mostra la procedura per l'avvicinamento e l'atterraggio strumentale su di una data pista, inclusi gli anelli di holding, i terminal VOR, gli ILS e le frequenze radio della torre.
La carta TAXI mostra le rampe di accesso alla pista e le aree di manovra e parcheggio a terra di un aeroporto. Nel nostro simulatore non serve.
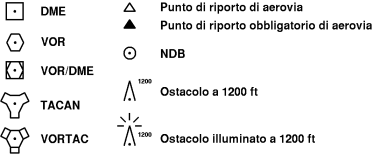
Illustriamo i principali simboli che si trovano nelle carte aeronautiche.
| Umberto Salsi | Commenti | Contatto | Mappa | Home / Indice sezione |
Still no comments to this page. Use the Comments link above to add your contribute.